Question

双曲线2x²-y²=1的渐近线方程是________．

Answer 1

分析：将双曲线化成标准方程，得到a、b的值，再由双曲线的渐近线方程是y=±x，即可得到所求渐近线方程．
解答：∵双曲线2x²-y²=1的标准方程为：
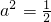∴，b²=1，可得a=，b=1
又∵双曲线的渐近线方程是y=±x
∴双曲线2x²-y²=1的渐近线方程是y=±x
故答案为：y=±x
点评：本题给出双曲线方程，求双曲线的渐近线方程，着重考查了双曲线的简单几何性质，属于基础题．