题目内容
5.某市为鼓励居民节约用水,将实行阶梯式计量水价,该市每户居民每月用水量划分为三档,水价实行分档递增.第一级水量:用水量不超过20吨,水价标准为1.60元/吨;
第二级水量:用水量超过20吨但不超过40吨,超出第一级水量的部分,水价标准比第一级水价提高0.8元/吨;
第三级水量:用水量超过40吨,超出第二级水量的部分,水价标准比第一级水价提高1.60元/吨.
随机调查了该市500户居民,获得了他们某月的用水量数据,整理得到如下的频率分布表:
| 用水量(吨) | [0,10] | (10,20] | (20,30] | (30,40] | (40,50] | 合计 |
| 频数 | 50 | 200 | 100 | b | 50 | 500 |
| 频率 | 0.1 | a | 0.2 | c | 0.1 | 1 |
(2)从该市调查的500户居民中随机抽取一户居民,求该户居民用水量不超过36吨的概率;
(3)假设同组中的每个数据用该组区间的中点值代替,试估计该市每户居民该月的平均水费.
分析 (1)由频率分布表能求出a,b,c.
(2)设“该户居民用水量不超过36吨”为事件A,由表能求出调查的500户居民中,用水量不超过36吨的概率.
(3)由用水量的频率分布表和题意,得居民该月用水费用的数据分组与频率分布表,由此能求出该市每户居民该月的平均水费.
解答 满分(12分)
解:(1)由频率分布表可得:
a=0.4,b=100,c=0.2.…(3分)
(2)设“该户居民用水量不超过36吨”为事件A,
由表可知,调查的500户居民中,用水量不超过36吨的概率为:
P(A)=0.1+0.4+0.2+0.2×$\frac{6}{10}$=0.82.…(7分)
(3)由用水量的频率分布表和题意,得居民该月用水费用的数据分组与频率分布表:
| 用水量(吨) | [0,10) | (10,20] | (20,30] | (30,40] | (40,50] |
| 用水费用 | [0,16] | (16,32] | (32,56] | (56,80] | (80,112] |
| 频率 | 0.1 | 0.4 | 0.2 | 0.2 | 0.1 |
8×0.1+24×0.4+44×0.2+68×0.2+96×0.1=42.4.(元)…(12分)
点评 本题主要考查茎叶图、中位数、平均数、方差、古典概型等基础知识;考查学生应用意识、运算求解能力、数据处理能力及分析问题解决问题的能力;考查了分类与整合思想、必然与或然的数学思想.

练习册系列答案
相关题目
13.锥体中,平行于底面的两个平面把锥体的体积三等分,这时高被分成三段的长自上而下的比为( )
| A. | 1:$\root{3}{2}$:$\root{3}{3}$ | B. | 1:2:3 | C. | 1:($\sqrt{2}$-1):($\sqrt{3}$-$\sqrt{2}$) | D. | 1:($\root{3}{2}$-1):($\root{3}{3}$-$\root{3}{2}$) |
20.已知函数f(x)=log${\;}_{\frac{1}{e}}}$(x2+$\frac{1}{e}}$)-|${\frac{x}{e}}$|,则使得f(x+1)<f(2x-1)的x的范围是( )
| A. | (0,2) | B. | (-∞,0) | C. | (-∞,0)∪(2,+∞) | D. | (2,+∞) |
8.设等差数列{an}的公差d≠0,a1=2d,若ak是a1与a2k+1的等比中项,则k=( )
| A. | 2 | B. | 3 | C. | 6 | D. | 8 |
 已知f(x)为定义在R上的奇函数,当x>0时,f(x)为二次函数,且满足f(2)=1,f(x)在x轴上的两个交点为(1,0)、(3,0).
已知f(x)为定义在R上的奇函数,当x>0时,f(x)为二次函数,且满足f(2)=1,f(x)在x轴上的两个交点为(1,0)、(3,0). 如图,四边形ABCD是边长为$\sqrt{2}$的正方形,CG⊥平面ABCD,DE∥BF∥CG,$DE=BF=\frac{3}{5}CG$.P为线段EF的中点,AP与平面ABCD所成角为60°.在线段CG上取一点H,使得$GH=\frac{3}{5}CG$.
如图,四边形ABCD是边长为$\sqrt{2}$的正方形,CG⊥平面ABCD,DE∥BF∥CG,$DE=BF=\frac{3}{5}CG$.P为线段EF的中点,AP与平面ABCD所成角为60°.在线段CG上取一点H,使得$GH=\frac{3}{5}CG$.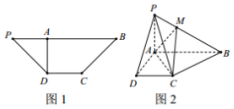 如图1,在等腰梯形PDCB中,PB∥DC,PB=3,DC=1,∠DPB=45°,DA⊥PB于点A,将△PAD沿AD折起,构成如图2所示的四棱锥P-ABCD,点M的棱PB上,且PM=$\frac{1}{2}$MB.
如图1,在等腰梯形PDCB中,PB∥DC,PB=3,DC=1,∠DPB=45°,DA⊥PB于点A,将△PAD沿AD折起,构成如图2所示的四棱锥P-ABCD,点M的棱PB上,且PM=$\frac{1}{2}$MB.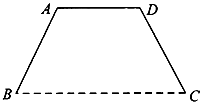 某单位将举办庆典活动,要在广场上竖立一形状为等腰梯形的彩门BADC (如图),设计要求彩门的面积为S (单位:m2)•高为h(单位:m)(S,h为常数),彩门的下底BC固定在广场地面上,上底和两腰由不锈钢支架构成,设腰和下底的夹角为α,不锈钢支架的长度和记为l.
某单位将举办庆典活动,要在广场上竖立一形状为等腰梯形的彩门BADC (如图),设计要求彩门的面积为S (单位:m2)•高为h(单位:m)(S,h为常数),彩门的下底BC固定在广场地面上,上底和两腰由不锈钢支架构成,设腰和下底的夹角为α,不锈钢支架的长度和记为l.