题目内容
函数y=
| ||
| |x+1|-2 |
分析:要函数y=
的解析式有意义,自变量须满足:4-x2≥0且|x+1|-2≠0,解不等式组,求出自变量x的取值范围,即可得到答案.
| ||
| |x+1|-2 |
解答:解:要使函数的解析式有意义,自变量须满足:
4-x2≥0且|x+1|-2≠0
解得-2≤x<1或1<x≤2
函数y=
的定义域为[-2,1)∪(1,2]
故答案为:[-2,1)∪(1,2]
4-x2≥0且|x+1|-2≠0
解得-2≤x<1或1<x≤2
函数y=
| ||
| |x+1|-2 |
故答案为:[-2,1)∪(1,2]
点评:本题考查的知识点是函数的定义域,当函数是由解析式给出时,其定义域是使解析式有意义的自变量的取值集合.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
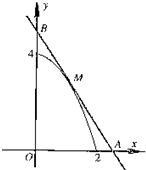 如图,已知M是函数y=4-x2(1<x<2)的图象C上一点,过M点作曲线C的切线与x轴、y轴分别交于点A,B,O是坐标原点,求△AOB面积的最小值.
如图,已知M是函数y=4-x2(1<x<2)的图象C上一点,过M点作曲线C的切线与x轴、y轴分别交于点A,B,O是坐标原点,求△AOB面积的最小值.