Question

已知函数的最小值为0。

（Ⅰ）求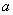的值；

（Ⅱ）若对任意的，有成立，求实数的最小值；

Answer 1

解：（Ⅰ）的定义域为，，

由，得，当变化时，，的变化情况如下表：

	－	0	＋
	↘	极小值	↗

因此，在处取得最小值，故由题意，所以。

（Ⅱ）当时，取，有，而，故不合题意；

当时，令，

，令，得，；

（1）当时，，在上恒成立，因此在上单调递减，从而对于任意的，总有，即在上恒成立，故符合题意。

（2）当时，，对于，，故在内单调递增，因此当取时，，即不成立，故不合题意。

综上，的最小值为。