题目内容
正四棱台的上、下底面边长分别是5和7,对角线长为9,则棱台的斜高等于分析:画出棱台图形,连接两底面中心o1、o,并连接A1O1和AO,过A1作A1E⊥AO于E,过E作EF⊥AB于F,则A1E为高,A1F为斜高,进而利用勾股定理可得答案.
解答: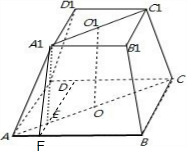 解:如图:连接两底面中心o1、o,并连接A1O1和AO,
解:如图:连接两底面中心o1、o,并连接A1O1和AO,
过A1作A1E⊥AO于E,过E作EF⊥AB于F,则A1E为高,A1F为斜高,
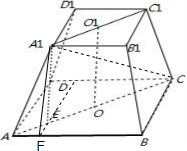
两底面的边长分别为5和7,
∴AC=7
,A1C1=5
,
则在Rt△A1EC中,CE=6
,A1C=9,
故A1E=
=3,
在Rt△A1EF中,EF=
(7-5)=1,
故A1F=
=
,
故答案为:
 解:如图:连接两底面中心o1、o,并连接A1O1和AO,
解:如图:连接两底面中心o1、o,并连接A1O1和AO,过A1作A1E⊥AO于E,过E作EF⊥AB于F,则A1E为高,A1F为斜高,

两底面的边长分别为5和7,
∴AC=7
| 2 |
| 2 |
则在Rt△A1EC中,CE=6
| 2 |
故A1E=
92-(6
|
在Rt△A1EF中,EF=
| 1 |
| 2 |
故A1F=
| 32+12 |
| 10 |
故答案为:
| 10 |
点评:本题考查棱台的结构特征,考查计算能力,作图能力,勾股定理的应用,是基础题.

练习册系列答案
相关题目
一个正四棱台的上、下底面边长分别为a、b,高为h,且侧面及等于两底面积之和,则下列关系正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|