题目内容
如图,已知在四边形ABCD中,AD⊥CD,AD=10,AB=14,∠BDA=60°,∠BCD=135°,求BC的长.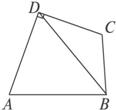
解:在△BCD中,由余弦定理有AB2=AD2+BD2-2·AD·BD·cos∠ADB.
设BD=x.
代入有
142=x2+102-2·10xcos60°,x2-10x-96=0.
∴x1=16,x2=-6(舍去),
即BD=16.
在△BCD中,由正弦定理
![]() =
=![]() ,
,
可得BC=![]() ·sin30°=8
·sin30°=8![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知四棱锥P-ABCD的底面ABCD是平行四边形,PA=AB=AD=a,
如图,已知四棱锥P-ABCD的底面ABCD是平行四边形,PA=AB=AD=a, 如图,已知空间四边形OABC,其对角线为OB、AC,M、N分别是对边OA、BC的中点,点G在线段MN上,且
如图,已知空间四边形OABC,其对角线为OB、AC,M、N分别是对边OA、BC的中点,点G在线段MN上,且 如图,已知直线
如图,已知直线 如图,已知空间四边形OABC,其对角线为OB、AC,M、N分别是对边OA、BC的中点,点G在线段MN上,且
如图,已知空间四边形OABC,其对角线为OB、AC,M、N分别是对边OA、BC的中点,点G在线段MN上,且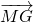 =2
=2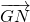 ,现用基向量
,现用基向量 ,
, ,
, 表示向量,设
表示向量,设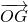 =x
=x ,y=
,y=
 BC,设
BC,设 =a,
=a, =b,试用a,b分别表示
=b,试用a,b分别表示 、
、 、
、 。
。