题目内容
设公差不为0的等差数列{an}的首项为1,且a2,a5,a14构成等比数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足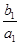 +
+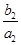 +…+
+…+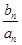 =1-
=1-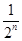 ,n∈N*,求{bn}的前n项和Tn.
,n∈N*,求{bn}的前n项和Tn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足
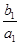 +
+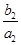 +…+
+…+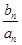 =1-
=1-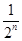 ,n∈N*,求{bn}的前n项和Tn.
,n∈N*,求{bn}的前n项和Tn.(Ⅰ)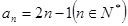 ;(Ⅱ)Tn=3-
;(Ⅱ)Tn=3-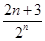 .
.
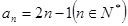 ;(Ⅱ)Tn=3-
;(Ⅱ)Tn=3-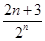 .
.试题分析:(Ⅰ)主要利用等差、等比的概念来求;(Ⅱ)可以构造新数列
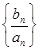 ,则
,则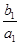 +
+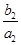 +…+
+…+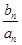 =1-
=1-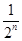 为其前
为其前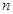 项和,通过
项和,通过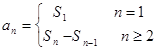 可求数列
可求数列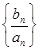 的通项公式,再根据
的通项公式,再根据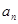 可求
可求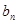 ,然后对其求和;
,然后对其求和;试题解析:(Ⅰ) 设等差数列{an}的公差为d(d≠0),则
∵a2,a5,a14构成等比数列,
∴
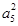 =a2a14,
=a2a14,即(1+4d)2=(1+d)(1+13d),
解得d=0(舍去),或d=2.
∴an=1+(n-1)×2=2n-1. 4分
(Ⅱ)由已知
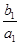 +
+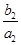 +…+
+…+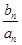 =1-
=1-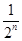 ,n∈N*,
,n∈N*,当n=1时,
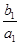 =
= ;
;当n≥2时,
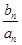 =1-
=1-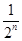 -(1-
-(1-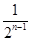 )=
)=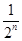 .
.∴
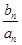 =
=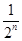 ,n∈N*.
,n∈N*.由(Ⅰ),知an=2n-1,n∈N*,
∴bn=
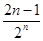 ,n∈N*.
,n∈N*.又Tn=
 +
+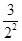 +
+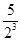 +…+
+…+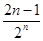 ,
, Tn=
Tn=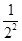 +
+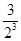 +…+
+…+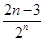 +
+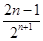 .
.两式相减,得
 Tn=
Tn= +(
+(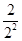 +
+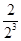 +…+
+…+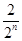 )-
)-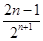 =
=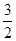 -
-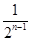 -
-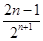 ,
,∴Tn=3-
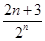 . 12分
. 12分
练习册系列答案
相关题目
 是数列
是数列 的前
的前 项和,
项和, ,
, ,
, .
. 是等差数列,并
是等差数列,并 ,求数列
,求数列 的前
的前 .
.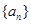 的各项均为正数,
的各项均为正数,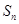 为其前
为其前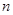 项和,对于任意的
项和,对于任意的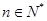 ,满足关系式
,满足关系式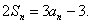
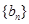 的通项公式是
的通项公式是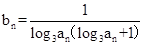 ,前
,前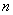 项和为
项和为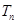 ,求证:对于任意的正整数
,求证:对于任意的正整数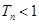 .
. (
( )的等差数列
)的等差数列 与公比为
与公比为 (
( )的等比数列
)的等比数列 有如下关系:
有如下关系: ,
, ,
, .
. ,
, ,
, ,求集合
,求集合 中的各元素之和。
中的各元素之和。 及其前
及其前 项和
项和 满足:
满足: (
( ,
, ).
). ,
, 是等差数列;(2)求
是等差数列;(2)求 及
及 .
.
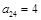 ,
,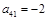 ,
,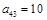 ,则
,则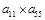 的值为__________
的值为__________ 满足:
满足: ,则
,则 = .
= .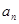 }的前21项的和等于前8项的和.若
}的前21项的和等于前8项的和.若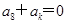 ,则k=( )
,则k=( ) 为等差数列,其前
为等差数列,其前 项和为
项和为 ,若
,若 ,
, ,则公差
,则公差 等于( )
等于( )


