题目内容
若函数f(x)＝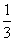
x3－
ax2＋(a－1)x＋1在区间(1,4)上为减函数，
在区间(6，＋∞)上为增函数，试求实数a的取值范围．
解 函数f(x)的导数 f′(x)＝x2－ax＋a－1.
令f′(x)＝0，解得x＝1，或x＝a－1.
当a－1≤1即a≤2时，函数f(x)在(1，＋∞)上为增函数，不合题意；
当a－1>1即a>2时，函数f(x)在(－∞，1)上为增函数，在(1，a－1)上为减函数，
在(a－1，＋∞)上为增函数．
依题意应有当x∈(1,4)时，f′(x)<0；
当x∈(6，＋∞)时，f′(x)>0.
所以4≤a－1≤6，解得5≤a≤7.
所以a的取
值范围为[5,7]．
练习册系列答案
相关题目
(ω>0)的图象如图所示，则ω＝__________.
所在直线经过点P
，则sin β＝________，tan β＝________.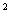
－mx (m∈R)，g(x)＝ln x.
在x
线方程是x－y＋1＝0，则a,b的值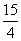
x－9都相切，求a的值．