题目内容
3.设a=cos127°cos50°+sin53°cos40°,b=$\frac{\sqrt{2}}{2}$(sin56°-cos56°),c=$\frac{1}{2}$(cos80°-2cos250°+1),则a、b、c的大小关系为( )| A. | a>b>c | B. | b>a>c | C. | a>c>b | D. | c>b>a |
分析 化简三角函数,然后判断三个数的大小.
解答 解:a=cos127°cos50°+sin53°cos40°
=-sin53°(sin40°+cos40°)=$\sqrt{2}$sin53°sin85°$>\sqrt{2}×\frac{\sqrt{2}}{2}×\frac{\sqrt{3}}{2}$$>\frac{\sqrt{3}}{2}$,
b=$\frac{\sqrt{2}}{2}$(sin56°-cos56°)=sin11°∈(0,$\frac{1}{2}$),
c=$\frac{1}{2}$(cos80°-2cos250°+1)=$\frac{1}{2}$(cos80°-cos100°)=sin10°,
sin11°>sin10°.
所以a>b>c.
故选:A.
点评 本题考查三角函数的化简求值,正弦函数的单调性,两角和与差的三角函数,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.设向量$\overrightarrow a$,$\overrightarrow b$满足$|\overrightarrow a|=1$,$|\overrightarrow a+\overrightarrow b|=\sqrt{3}$,$\overrightarrow a•(\overrightarrow a+\overrightarrow b)=0$,则$|2\overrightarrow a-\overrightarrow b|$=( )
| A. | 2 | B. | $2\sqrt{3}$ | C. | 4 | D. | $4\sqrt{3}$ |
11.设抛物线y2=8x的焦点为F,M是抛物线上一点,N(2,2),则|MF|+|MN|的取值范围是( )
| A. | (0,4] | B. | [4,+∞) | C. | (0,2] | D. | [2,+∞) |
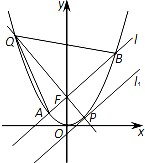 如图,过抛物线C:x2=2py(p>0)的焦点F作直线l与抛物线相交于A,B两点.直线l1∥l,且与抛物线C相切于点P,直线PF交抛物线于另一点Q.已知抛物线C上纵坐标为$\frac{3p}{2}$的点M到焦点F的距离为2.
如图,过抛物线C:x2=2py(p>0)的焦点F作直线l与抛物线相交于A,B两点.直线l1∥l,且与抛物线C相切于点P,直线PF交抛物线于另一点Q.已知抛物线C上纵坐标为$\frac{3p}{2}$的点M到焦点F的距离为2.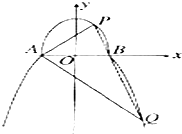 如图,曲线C由上半椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0,y≥0)和部分抛物线C2:y=-x2+1(y≤0)连接而成,C1、C2的公共点为A,B,其中C1的离心率为$\frac{\sqrt{3}}{2}$.
如图,曲线C由上半椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0,y≥0)和部分抛物线C2:y=-x2+1(y≤0)连接而成,C1、C2的公共点为A,B,其中C1的离心率为$\frac{\sqrt{3}}{2}$.