题目内容
【题目】在直角坐标系xOy中,圆C的参数方程为:![]() 为参数
为参数![]() ,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,射线l的极坐标方程为
,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,射线l的极坐标方程为![]() ,
,![]() .
.
![]() 将圆C的参数方程化为极坐标方程;
将圆C的参数方程化为极坐标方程;
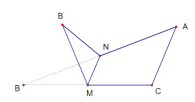
![]() 设点A的直角坐标为
设点A的直角坐标为![]() ,射线l与圆C交于点
,射线l与圆C交于点![]() 不同于点
不同于点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
![]() 圆C的参数方程消去参数,能求出圆C的普通方程,由此能求出圆C的极坐标方程;
圆C的参数方程消去参数,能求出圆C的普通方程,由此能求出圆C的极坐标方程;![]() 求出
求出![]() ,
,![]() ,
,![]() ,分情况讨论,当
,分情况讨论,当![]() 时,能求出
时,能求出![]() 面积的最大值.
面积的最大值.
![]() 圆C的参数方程为:
圆C的参数方程为:![]() 为参数
为参数![]() ,
,
![]() 圆C的普通方程为
圆C的普通方程为![]() ,即
,即![]() ,
,
![]() 圆C的极坐标方程为
圆C的极坐标方程为![]() ,即
,即![]() .
.
![]() 射线l的极坐标方程为
射线l的极坐标方程为![]() ,
,![]() 射线l与圆C交于点
射线l与圆C交于点![]() 不同于点
不同于点![]() ,
,
![]() ,
,![]() ,
,
![]() 点A的直角坐标为
点A的直角坐标为![]() ,
,![]() ,
,
分两种情况:当![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]() 当
当![]() ,即
,即![]() 时,
时,
![]() 面积取最大值
面积取最大值![]() .
.
当![]() ,
,![]() )
)
=![]() )
)
=![]()
![]() 当
当![]() ,即
,即![]() 时三角形的面积最大值为:
时三角形的面积最大值为:![]()
![]() <
<![]() .此时也不符合:
.此时也不符合:![]() .
.
综上面积的大值为:![]() .
.

【题目】北京地铁八通线西起四惠站,东至土桥站,全长![]() ,共设13座车站
,共设13座车站![]() 目前八通线执行2014年12月28日制订的计价标准,各站间计程票价
目前八通线执行2014年12月28日制订的计价标准,各站间计程票价![]() 单位:元
单位:元![]() 如下:
如下:
四惠 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | |
四惠东 | 3 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | ||
高碑店 | 3 | span>3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | |||
传媒大学 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | ||||
双桥 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | |||||
管庄 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | ||||||
八里桥 | 3 | 3 | 3 | 3 | 4 | 4 | |||||||
通州北苑 | 3 | 3 | 3 | 3 | 3 | ||||||||
果园 | 3 | 3 | 3 | 3 | |||||||||
九棵树 | 3 | 3 | 3 | ||||||||||
梨园 | 3 | 3 | |||||||||||
临河里 | 3 | ||||||||||||
土桥 | |||||||||||||
四惠 | 四惠东 | 高碑店 | 传媒大学 | 双桥 | 管庄 | 八里桥 | 通州北苑 | 果园 | 九棵树 | 梨园 | 临河里 | 土桥 |
![]() 1
1![]() 在13座车站中任选两个不同的车站,求两站间票价为5元的概率;
在13座车站中任选两个不同的车站,求两站间票价为5元的概率;
![]() 2
2![]() 在土桥出站口随机调查了n名下车的乘客,将在八通线各站上车情况统计如下表:
在土桥出站口随机调查了n名下车的乘客,将在八通线各站上车情况统计如下表:
上车站点 | 通州北苑
| 双桥 | 四惠
|
频率 |
| a | b |
人数 | c | 15 | 25 |
求a,b,c,n的值,并计算这n名乘客乘车平均消费金额;
![]() 3
3![]() 某人从四惠站上车乘坐八通线到土桥站,中途任选一站出站一次,之后再从该站乘车
某人从四惠站上车乘坐八通线到土桥站,中途任选一站出站一次,之后再从该站乘车![]() 若想两次乘车花费总金额最少,可以选择中途哪站下车?
若想两次乘车花费总金额最少,可以选择中途哪站下车?![]() 写出一个即可
写出一个即可![]()