题目内容
若|a|＜1,|b|＜1,求证:|
|＜1.
证明:假设||≥1,则|a+b|≥|1+ab|.
∴a2+b2+2ab≥1+2ab+a2b2.
∴a2+b2-a2b2-1≥0.
∴a2-1-b2(a2-1)≥0.
∴(a2-1)(1-b2)≥0.
∴
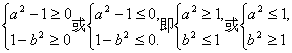
即a2≥1,b2≤1或a2≤1,b2≥1,与已知矛盾.
∴|
|＜1.
练习册系列答案
相关题目
|＜1.题目内容
若|a|＜1,|b|＜1,求证:||＜1.
证明:假设||≥1,则|a+b|≥|1+ab|.
∴a2+b2+2ab≥1+2ab+a2b2.
∴a2+b2-a2b2-1≥0.
∴a2-1-b2(a2-1)≥0.
∴(a2-1)(1-b2)≥0.
∴
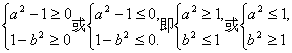
即a2≥1,b2≤1或a2≤1,b2≥1,与已知矛盾.
∴||＜1.
=a，
1=b，
=c，则
=__________________.
-2
= 
和两个不重合的平面α、β，下列命题中正确命题个数为（ ）
②
④