题目内容
14.函数f(x)=sinx+2|sinx|,(x∈(0,2π)的图象与直线y=k恰有四个不同的交点,则k的取值范围是(0,1).分析 画出函数f(x)(x∈[0,2π])以及直线y=k 的图象,数形结合可得k的取值范围.
解答 解:画出函数f(x)=2|sinx|+sinx=$\left\{\begin{array}{l}{3sinx,x∈[0,π)}\\{-sinx,x∈[π,2π]}\end{array}\right.$,(x∈[0,2π])以及直线y=k 的图象,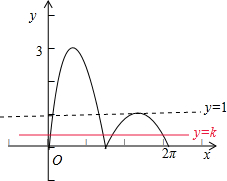
由f(x)的图象与直线y=k有且仅有四个不同的交点,可得0<k<1,
故答案为:(0,1).
点评 本题主要考查正弦函数的图象,体现了数形结合的数学思想,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.执行如图所示的程序框图,若输出的值为y=5,则满足条件的实数x的个数为( )

| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
6.已知函数$f(x)=\left\{\begin{array}{l}a•{2^x},x≥0\\{2^{-x}},x<0\end{array}\right.$(a∈R),若f(f(-1))=1,则a=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
3.设曲线$\left\{\begin{array}{l}{x=2cosθ}\\{y=\sqrt{3}sinθ}\end{array}\right.$与x轴交点为M、N,点P在曲线上,则PM与PN所在直线的斜率之积为( )
| A. | -$\frac{3}{4}$ | B. | -$\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |