题目内容
弹性题:已知函数f(x)在(0,+∞)上有意义,且满足下列条件:①f(x)在(0,+∞)上递减,且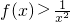 ;②在(0,+∞)上在恒有
;②在(0,+∞)上在恒有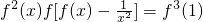 .
.
(1)求f(1);
(2)写出一个满足题设条件的函数f(x).
解:(1)由已知得
∴f[f(1)-1]=f(1)
又f(x)在(0,+∞)上是减函数,
∴f(1)-1=1即
∴f(1)=2
(2)设 ,
,
∵f(1)=2
∴a=2,可证明 在(0,+∞)上是减函数,符合条件(1)又
在(0,+∞)上是减函数,符合条件(1)又 ,符合条件(2)
,符合条件(2)
∴ 满足题设的两个条件.
满足题设的两个条件.
分析:(1)由 ,知f[f(1)-1]=f(1),由f(x)在(0,+∞)上是减函数,能求出f(1).
,知f[f(1)-1]=f(1),由f(x)在(0,+∞)上是减函数,能求出f(1).
(2)设 ,由f(1)=2,知a=2,可证明
,由f(1)=2,知a=2,可证明 在(0,+∞)上是减函数,
在(0,+∞)上是减函数, ,所以
,所以 满足题设的两个条件.
满足题设的两个条件.
点评:本题考查函数值的求法,写出一个满足题设条件的函数f(x).解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

∴f[f(1)-1]=f(1)
又f(x)在(0,+∞)上是减函数,
∴f(1)-1=1即
∴f(1)=2
(2)设
 ,
,∵f(1)=2
∴a=2,可证明
 在(0,+∞)上是减函数,符合条件(1)又
在(0,+∞)上是减函数,符合条件(1)又 ,符合条件(2)
,符合条件(2)∴
 满足题设的两个条件.
满足题设的两个条件.分析:(1)由
 ,知f[f(1)-1]=f(1),由f(x)在(0,+∞)上是减函数,能求出f(1).
,知f[f(1)-1]=f(1),由f(x)在(0,+∞)上是减函数,能求出f(1).(2)设
 ,由f(1)=2,知a=2,可证明
,由f(1)=2,知a=2,可证明 在(0,+∞)上是减函数,
在(0,+∞)上是减函数, ,所以
,所以 满足题设的两个条件.
满足题设的两个条件.点评:本题考查函数值的求法,写出一个满足题设条件的函数f(x).解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目
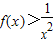 ;②在(0,+∞)上在恒有
;②在(0,+∞)上在恒有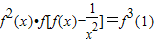 .
.