题目内容
弹性题:已知函数f(x)在(0,+∞)上有意义,且满足下列条件:①f(x)在(0,+∞)上递减,且f(x)>
;②在(0,+∞)上在恒有f2(x)•f[f(x)-
]=f3(1).
(1)求f(1);
(2)写出一个满足题设条件的函数f(x).
| 1 |
| x2 |
| 1 |
| x2 |
(1)求f(1);
(2)写出一个满足题设条件的函数f(x).
(1)由已知得
∴f[f(1)-1]=f(1)
又f(x)在(0,+∞)上是减函数,
∴f(1)-1=1即
∴f(1)=2
(2)设f(x)=
,
∵f(1)=2
∴a=2,可证明f(x)=
在(0,+∞)上是减函数,符合条件(1)又f2(x)f[f(x)-
]=(
)2f(
-
)=
f(
)=8=f3(1),符合条件(2)
∴f(x)=
满足题设的两个条件.
|
∴f[f(1)-1]=f(1)
又f(x)在(0,+∞)上是减函数,
∴f(1)-1=1即
∴f(1)=2
(2)设f(x)=
| a |
| x2 |
∵f(1)=2
∴a=2,可证明f(x)=
| 2 |
| x2 |
| 1 |
| x2 |
| 2 |
| x2 |
| 2 |
| x2 |
| 1 |
| x2 |
| 4 |
| x2 |
| 1 |
| x2 |
∴f(x)=
| 2 |
| x2 |

练习册系列答案
相关题目
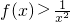 ;②在(0,+∞)上在恒有
;②在(0,+∞)上在恒有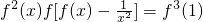 .
.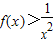 ;②在(0,+∞)上在恒有
;②在(0,+∞)上在恒有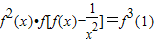 .
.