题目内容
设集合A＝{(x，y)|(x－4)2＋y2＝1}，B＝{(x，y)|(x－t)2＋(y－at＋2)2＝1}，若存在实数t，使得A∩B≠∅，则实数a的取值范围是________．
[解析] 集合A表示的是以(4,0)为圆心，以1为半径的圆，集合B表示的是以(t，at－2)为圆心，以1为半径的圆．
A∩B≠∅说明这两个圆至少有一个交点，故
≤1＋1＝2，即(a2＋1)t2－4(a＋2)t＋16≤0，据题意此不等式有实数解，故判别式Δ＝16(a＋2)2－4(a2＋1)×16≥0，即3a2－4a≤0，解得0≤a≤
.
练习册系列答案
阅读快车系列答案
相关题目
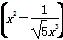5的展开式中的常数项为T，f(x)是以T为周期的偶函数，且当x∈[0,1]时，f(x)＝x，若在区间[－1,3]内，函数g(x)＝f(x)－kx－k有4个零点，则实数k的取值范围是________．
的不同值的个数是( )
2”的充要条件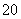
＋x0＋1＜0，则綈p：∀x∈R，x2＋x＋1≥0
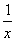在其定义域上是减函数