题目内容
(2013•浙江)如图F1、F2是椭圆C1: +y2=1与双曲线C2的公共焦点A、B分别是C1、C2在第二、四象限的公共点,若四边形AF1BF2为矩形,则C2的离心率是( )
+y2=1与双曲线C2的公共焦点A、B分别是C1、C2在第二、四象限的公共点,若四边形AF1BF2为矩形,则C2的离心率是( )
A. B.
B.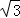 C.
C. D.
D.
D
解析

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
(2011•湖北)将两个顶点在抛物线y2=2px(p>0)上,另一个顶点是此抛物线焦点的正三角形个数记为n,则( )
| A.n=0 | B.n=1 | C.n=2 | D.n≥3 |
设双曲线 的渐近线方程为
的渐近线方程为 ,则
,则 的值为( )
的值为( )
| A.4 | B.3 | C.2 | D.1 |
已知点F1、F2分别是双曲线 =1(a>0,b>0)的左、右焦点,过F1且垂直于x轴的直线与双曲线交于A,B两点,若△ABF2是锐角三角形,则该双曲线离心率的取值范围是( )
=1(a>0,b>0)的左、右焦点,过F1且垂直于x轴的直线与双曲线交于A,B两点,若△ABF2是锐角三角形,则该双曲线离心率的取值范围是( )
A.(1, ) ) | B.( ,2 ,2 ) ) |
C.(1+ ,+∞) ,+∞) | D.(1,1+ ) ) |
双曲线 (m>0,n>0)的离心率为2,有一个焦点与抛物线y2=4mx的焦点重合,则n的值为( )
(m>0,n>0)的离心率为2,有一个焦点与抛物线y2=4mx的焦点重合,则n的值为( )
| A.1 | B.4 | C.8 | D.12 |
抛物线y=﹣x2上的点到直线4x+3y﹣8=0距离的最小值是( )
A. | B. | C. | D.3 |
若m是2和8的等比中项,则圆锥曲线 的离心率是( )
的离心率是( )
A. | B.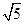 |
C. 或 或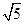 | D. |
 的左、右焦点,若双曲线右支上存在一点M,使
的左、右焦点,若双曲线右支上存在一点M,使 ,O为坐标原点,且
,O为坐标原点,且 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )



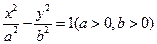 的左、右焦点分别为F1、F2,A是双曲线渐近线上的一点,AF1⊥AF2,原点O到直线AF1的距离为
的左、右焦点分别为F1、F2,A是双曲线渐近线上的一点,AF1⊥AF2,原点O到直线AF1的距离为 |OF1|,则双曲线的离心率为( )
|OF1|,则双曲线的离心率为( ) +1
+1