题目内容
已知函数 ,其中
,其中 是自然对数的底数,
是自然对数的底数, .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)当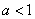 时,试确定函数
时,试确定函数 的零点个数,并说明理由.
的零点个数,并说明理由.
(Ⅰ)解:因为 ,
, ,
,
所以 .
.
令 ,得
,得 .
.
当 变化时,
变化时, 和
和 的变化情况如下:
的变化情况如下:
|
|
|
|
|
|
|
|
|
|
|
| ↘ | ↗ |
故 的单调减区间为
的单调减区间为 ;单调增区间为
;单调增区间为 .
.
(Ⅱ)解:结论:函数 有且仅有一个零点.
有且仅有一个零点.
理由如下:
由 ,得方程
,得方程 ,
,
显然 为此方程的一个实数解.
为此方程的一个实数解.
所以 是函数
是函数 的一个零点.
的一个零点.
当 时,方程可化简为
时,方程可化简为 .
.
设函数 ,则
,则 ,
,
令 ,得
,得 .
.
当 变化时,
变化时, 和
和 的变化情况如下:
的变化情况如下:
|
|
|
|
|
|
|
|
|
|
|
| ↘ | ↗ |
即 的单调增区间为
的单调增区间为 ;单调减区间为
;单调减区间为 .
.
所以 的最小值
的最小值 .
.
因为 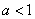 ,
,
所以 ,
,
所以对于任意 ,
, ,
,
因此方程 无实数解.
无实数解.
所以当 时,函数
时,函数 不存在零点.
不存在零点.
综上,函数 有且仅有一个零点.
有且仅有一个零点.

 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案已知函数满足,当时,,若在区间上方程有两个不同的实根,则实数的取值范围是( )
| A. | B. | C. | D. |
某中学对高二甲、乙两个同类班级进行“加强‘语文阅读理解’训练对提高‘数学应用题’得分率作用”的试验,其中甲班为试验班(加强语文阅读理解训练),乙班为对比班(常规教学,无额外训练),在试验前的测试中,甲、乙两班学生在数学应用题上的得分率基本一致,试验结束后,统计几次数学应用题测试的平均成绩(均取整数)如下表所示:
| 60分以下 | 61~70分 | 71~80分 | 81~90分 | 91~100分 | |
| 甲班(人数) | 3 | 6 | 11 | 18 | 12 |
| 乙班(人数) | 4 | 8 | 13 | 15 | 10 |
现规定平均成绩在80分以上(不含80分)的为优秀.
(Ⅰ)试分析估计两个班级的优秀率;
(Ⅱ)由以上统计数据填写下面2×2列联表,并问是否有75%的把握认为“加强‘语文阅读理解’训练对提高‘数学应用题’得分率”有帮助.
| 优秀人数 | 非优秀人数 | 合计 | |
| 甲班 | |||
| 乙班 | |||
| 合计 |
参考公式及数据: ,
,
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 |
| P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |













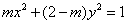 表示焦点在
表示焦点在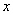 轴上的椭圆,则实数
轴上的椭圆,则实数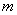 的取值范围是( )
的取值范围是( )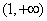 (B)
(B)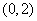 (C)
(C)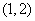 (D)
(D)
 为焦点在
为焦点在 ,
, 满足( )
满足( ) (B)
(B) (C)
(C) (D)
(D)
 为圆
为圆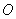 上的两个点,
上的两个点, 为
为 延长线上一点,
延长线上一点, 为圆
为圆 为切点. 若
为切点. 若 ,
, ,则
,则 ______;
______; ______.
______.
 那么
那么 等于
等于 B.
B. C.
C.  D.
D.
 B.
B. C.
C.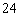 D.
D.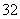
 :
: ,直线
,直线 与圆
与圆 ,
, 两点.
两点. ,且
,且 ,求直线
,求直线 为直径的圆经过原点,求直线
为直径的圆经过原点,求直线