题目内容
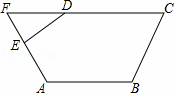
已知a，b不共线，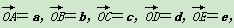
，设t∈R，如果3a＝c,2b＝d，e＝t(a＋b)，是否存在实数t使C，D，E三点在一条直线上？若存在，求出实数t的值；若不存在，请说明理由．
解 由题设知，
＝e－c＝(t－3)a＋tb，C，D，E三点在一条直线上的充要条件是存在实数k，使得
，即(t－3)a＋tb＝－3ka＋2kb.
整理得(t－3＋3k)a＝(2k－t)b.
因为a，b不共线，所以有
解得t＝
.
故存在实数t＝使C，D，E三点在一条直线上．
练习册系列答案
智趣暑假温故知新系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
B．y＝cos
D．y＝cos
，则
的最大值为( )
B.
sinB＝2sinC，则cosC的最小值是________．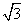
，BC＝2，点E在线段CD上，若
，则μ的取值范围是( )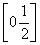
D.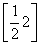
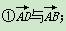
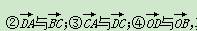其中可作为这个平行四边形所在平面的一组基底的是( )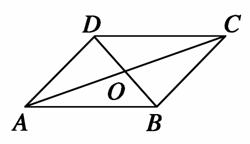
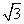)，O为坐标原点，C在第二象限，且∠AOC＝30°，
＝λ
＋
，则实数λ的值为________．
，
＝120.
求x，y的值．