Question

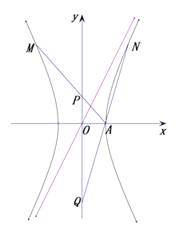
【题目】已知焦点在x轴上的双曲线C的两条渐近线过坐标原点，且两条渐近线与以点为圆心，1为半径的圆相切，又知C的一个焦点与P关于直线对称.

（1）求双曲线C的方程；

（2）设直线与双曲线C的左支交于A、B两点，另一直线经过及AB的中点，求直线在y轴上的截距b的取值范围；

（3）若Q是双曲线C上的任一点，、为双曲线C的左、右两个焦点，从引的角平分线的垂线，垂足为N，试求点N的轨迹方程.

Answer 1

【答案】（1）；（2）；（3），.

【解析】

（1）设双曲线的渐近线方程为，则，由该直线与圆相切，知双曲线的两条渐近线方程为．由此利用双曲线的一个焦点为，能求出双曲线的方程．

（2）由，得．令．直线与双曲线左支交于两点，等价于方程在上有两个不等实根．由此能求出直线在轴上的截距的取值范围．

（3）若在双曲线的右支上，则延长到，使，若在双曲线的左支上，则在上取一点，使．由此能求出点的轨迹方程．

（1）设双曲线的渐近线方程为，则，

该直线与圆相切，

双曲线的两条渐近线方程为．

故设双曲线的方程为．

又双曲线的一个焦点为，

，．

双曲线的方程为．

（2）由，得．

令

直线与双曲线左支交于两点，等价于方程在上有两个不等实根．

因此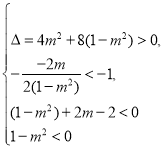，解得．

又中点为，

因为直线与轴相交，所以，即，

直线的方程为．

令，得．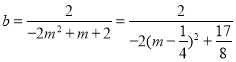

，

，

．

（3）若在双曲线的右支上，

则延长到，使，

若在双曲线的左支上，

则在上取一点，使．

根据双曲线的定义，

所以点在以为圆心，2为半径的圆上，

即点的轨迹方程是①

由于点是线段的中点，

设，，．

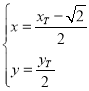则，即．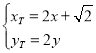

代入①并整理得点的轨迹方程为.