题目内容
(本小题满分13分)设函数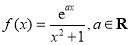 .
.
(Ⅰ)当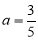 时,求函数
时,求函数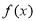 的单调区间;
的单调区间;
(Ⅱ)设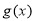 为
为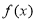 的导函数,当
的导函数,当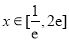 时,函数
时,函数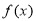 的图象总在
的图象总在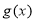 的图象的上方,求
的图象的上方,求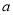 的取值范围.
的取值范围.
(1)函数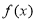 的单调增区间为
的单调增区间为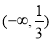 ,
,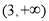 ;单调递减区间为
;单调递减区间为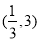 ;(2)
;(2)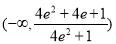 .
.
【解析】
试题分析:本题主要考查导数的运算、利用导数判断函数的单调性、利用导数求函数的最值、恒成立问题等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,先将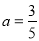 代入,利用导数除法的运算法则计算
代入,利用导数除法的运算法则计算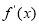 ,令
,令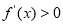 解出函数的增区间,令
解出函数的增区间,令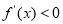 解出函数的减区间;第二问,先写出
解出函数的减区间;第二问,先写出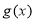 解析式,由于函数
解析式,由于函数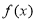 的图象总在
的图象总在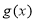 的图象的上方,所以
的图象的上方,所以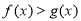 ,转化为
,转化为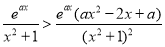 在
在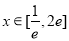 恒成立,继续转化为
恒成立,继续转化为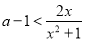 恒成立,构造函数
恒成立,构造函数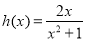 ,通过求导判断函数的单调区间,求出
,通过求导判断函数的单调区间,求出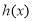 的最小值,最后解出a的取值范围.
的最小值,最后解出a的取值范围.
试题解析:(1)当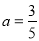 时,
时, .
.
∵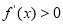 ,得
,得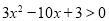 ,解得
,解得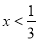 或
或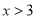 ;
;
∵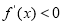 ,得
,得 ,解得
,解得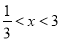 .
.
∴函数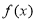 的单调增区间为
的单调增区间为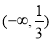 ,
,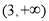 ;单调递减区间为
;单调递减区间为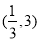 .
.
(2)∵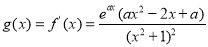 .
.
又∵函数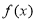 的图象总在
的图象总在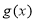 的图象的上方,
的图象的上方,
∴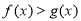 ,即
,即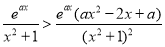 在
在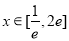 恒成立.
恒成立.
又∵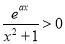 ,∴
,∴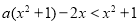 ,∴
,∴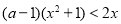 .
.
又∵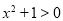 ,∴
,∴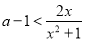 .
.
设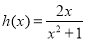 ,则
,则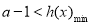
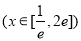 即可.
即可.
∵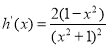 .
.
∵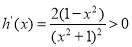 ,
,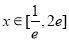 ,解得
,解得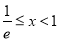 ;
;
∵ ,
,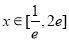 ,解得
,解得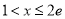 .
.
∴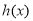 在区间
在区间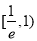 单调递增,在区间
单调递增,在区间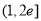 单调递减.
单调递减.
∴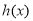 的最小值为
的最小值为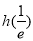 或
或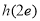 .
.
∵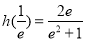 ,
,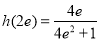 ,作差可知
,作差可知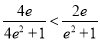 ,
,
∴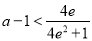 .
.
∴a的取值范围是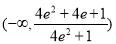 .
.
考点:导数的运算、利用导数判断函数的单调性、利用导数求函数的最值、恒成立问题.

练习册系列答案
相关题目
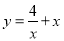 的最大值是 ( )
的最大值是 ( )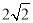 B.4 C.-4 D.-
B.4 C.-4 D.- 的左顶点为圆心,且与双曲线的渐近线相切的圆的方程为
的左顶点为圆心,且与双曲线的渐近线相切的圆的方程为  ,
, ,则向量
,则向量 在向量
在向量 方向上的投影是 .
方向上的投影是 . 中,
中, ,
, ,
, ,则A等于
,则A等于 (B)
(B)
 (D)
(D) 或
或
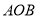 的边
的边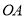 上有异于顶点
上有异于顶点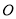 的6个点,边
的6个点,边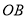 上有异于顶点
上有异于顶点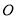 ,以这11个点为顶点共可以组成 个三角形(用数字作答).
,以这11个点为顶点共可以组成 个三角形(用数字作答). 中,
中, ,则
,则 的最大值是( )
的最大值是( ) B.
B. C.
C. D.
D.
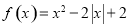 的定义域是
的定义域是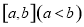 ,值域是
,值域是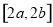 ,则符合条件的数组
,则符合条件的数组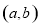 的组数为( )
的组数为( )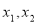
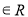 ,常数
,常数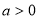 ,定义运算“*”:
,定义运算“*”: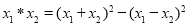 ,若
,若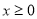 ,则动点P(
,则动点P(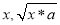 )的轨迹是( )
)的轨迹是( )