题目内容
12.已知函数$y=\frac{{|{{x^2}-1}|}}{x-1}$的图象与函数y=2x+b的图象恰有两个交点,则实数b的取值范围是(-4,0).分析 先化简函数的解析式,在同一个坐标系下画出函数$y=\frac{{|{{x^2}-1}|}}{x-1}$的图象与函数y=2x+b图象,结合图象,可得实数b的取值范围.
解答 解:当x>1或x<-1时,y=x+1,
当-1≤x<1时,y=-x+1,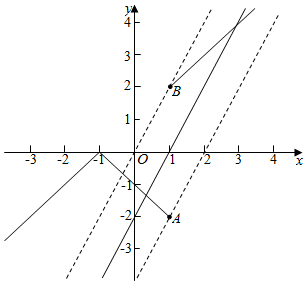
当直线y=2x+b经过点A(1,-2)时,此时-2=2+b,解得b=-4时只有一个交点,
当直线y=2x+b经过点B(,2)时,此时2=2+b,解得b=0,此时只有一个交点,
由图象可知,函数$y=\frac{{|{{x^2}-1}|}}{x-1}$的图象与函数y=2x+b的图象恰有两个交点,则实数b的取值范围是(-4,0)
故答案为:(-4,0).
点评 本题主要考查了根的存在性及根的个数判断,同时考查了作图能力和分类讨论的数学思想,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知直线l过(0,3),且与直线x+y+1=0垂直,则直线l的方程是( )
| A. | x+y-2=0 | B. | x-y+3=0 | C. | x+y-3=0 | D. | x-y+2=0 |
17.定义在N*的函数f(x)满足f(1)=2且有f(n+1)=$\left\{\begin{array}{l}\frac{1}{2}f(n),n为偶数\\ f(n),n为奇数\end{array}$,则f(12)的值为( )
| A. | $\frac{1}{32}$ | B. | $\frac{1}{16}$ | C. | $\frac{1}{64}$ | D. | 1 |
4.如图所示的程序框图,其作用是输入x的值,输出相应的y值,若输入$x=\frac{π}{2}$,则输出的y值为( )
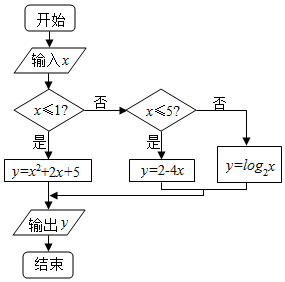

| A. | 2 | B. | ${log_2}\frac{π}{2}$ | C. | 2-2π | D. | 8 |
2.执行如图所示的程序框图,如果输入的x=t=3,则输出的M等于( )
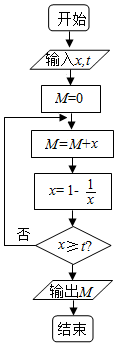

| A. | 3 | B. | $\frac{11}{3}$ | C. | $\frac{19}{6}$ | D. | $\frac{37}{6}$ |