题目内容
已知函数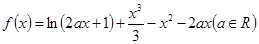
(Ⅰ)若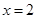 为
为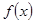 的极值点,求实数
的极值点,求实数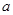 的值;
的值;
(Ⅱ)若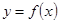 在
在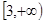 上为增函数,求实数
上为增函数,求实数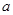 的取值范围;
的取值范围;
(Ⅲ)当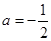 时,方程
时,方程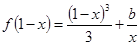 有实根,求实数
有实根,求实数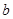 的最大值.
的最大值.
【答案】
(Ⅰ)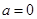 (Ⅱ)
(Ⅱ)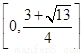 (Ⅲ)0
(Ⅲ)0
【解析】
试题分析:(I) ……2分
……2分
因为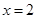 为
为 的极值点,所以
的极值点,所以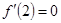 ,即
,即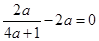 ,
,
解得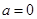 。经检验,合题意……4分(没有写经检验的减1分)
。经检验,合题意……4分(没有写经检验的减1分)
(II)因为函数 在
在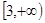 上为增函数,所以
上为增函数,所以
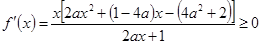 在
在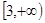 上恒成立。
上恒成立。
?当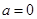 时,
时,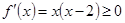 在
在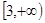 上恒成立,所以
上恒成立,所以 在
在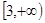 上为增函数,故
上为增函数,故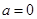 符合题意。 ……………………6分
符合题意。 ……………………6分
?当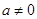 时,由函数
时,由函数 的定义域可知,必须有
的定义域可知,必须有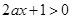 对
对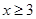 恒成立,
恒成立,
故只能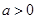 ,所以
,所以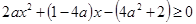 在
在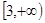 上恒成立。
上恒成立。
令函数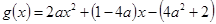 ,其对称轴为
,其对称轴为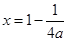 ,
,
因为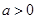 ,所以
,所以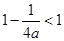 ,
,
要使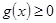 在
在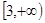 上恒成立,
上恒成立,
只要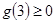 即可,即
即可,即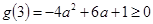 ,
,
所以 。
。
因为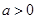 ,所以
,所以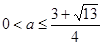 。
。
综上所述,a的取值范围为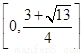 。………8分
。………8分
(Ⅲ)当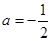 时,方程
时,方程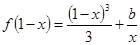 可化为
可化为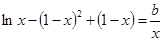 。
。
问题转化为 在
在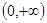 上有解,即求函数
上有解,即求函数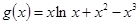 的值域。
的值域。
因为函数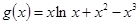 ,令函数
,令函数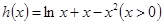 ,………10分
,………10分
则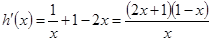 ,
,
所以当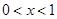 时,
时,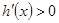 ,从而函数
,从而函数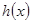 在
在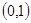 上为增函数,
上为增函数,
当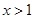 时,
时,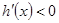 ,从而函数
,从而函数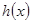 在
在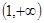 上为减函数,
上为减函数,
因此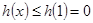 。
。
而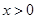 ,所以
,所以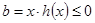 ,因此当
,因此当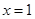 时,b取得最大值0. ………12分
时,b取得最大值0. ………12分
考点:函数导数的几何意义及利用导数求极值最值
点评:本题中的不等式恒成立或方程有实根转化为求构造的新函数的最值问题,这是函数题中最常用的转化方法

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
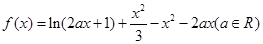
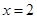 为
为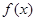 的极值点,求实数
的极值点,求实数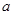 的值;
的值;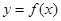 在
在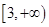 上为增函数,求实数
上为增函数,求实数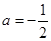 时,方程
时,方程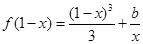 有实根,求实数
有实根,求实数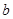 的最大值.
的最大值.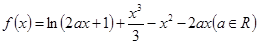
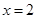 为
为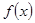 的极值点,求实数
的极值点,求实数 的值;
的值;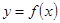 在
在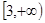 上为增函数,求实数
上为增函数,求实数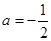 时,方程
时,方程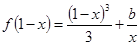 有实根,求实数
有实根,求实数 的最大值。
的最大值。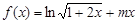 .
.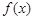 为定义域上的单调函数,求实数m的取值范围;
为定义域上的单调函数,求实数m的取值范围; 时,求函数
时,求函数 ,且
,且 时,证明:
时,证明: .
. .
. 为
为 的极值点,求实数
的极值点,求实数 的值;
的值; 上为增函数,求实数
上为增函数,求实数 时,方程
时,方程 有实根,求实数
有实根,求实数 的取值范围.
的取值范围.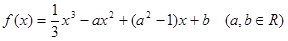 .
.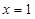 为
为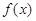 的极值点,求
的极值点,求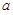 的值;
的值;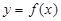 的图象在点(
的图象在点(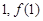 )处的切线方程为
)处的切线方程为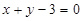 ,求
,求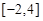 上的最大值;
上的最大值;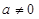 时,若
时,若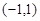 上不单调,求
上不单调,求