题目内容
2.已知F1(-4,0),F2(4,0),动点P满足||PF1|-|PF2||=4,则点P的轨迹方程为( )| A. | $\frac{x^2}{4}-\frac{y^2}{12}=1$ | B. | $\frac{x^2}{12}-\frac{y^2}{4}=1$ | C. | $\frac{y^2}{4}-\frac{x^2}{12}=1$ | D. | $\frac{y^2}{12}-\frac{x^2}{4}=1$ |
分析 由条件知,点P的轨迹是以F1、F2为焦点的双曲线,从而写出轨迹的方程即可.
解答 解:由||PF1|-|PF2||=4<|F1F2|知,点P的轨迹是以F1、F2为焦点的双曲线,c=4,2a=4,
∴a=2,
∴b2=12,
故动点P的轨迹方程是$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{12}$=1.
故选:A.
点评 本题考查双曲线的定义、求双曲线的标准方程,体现了等价转化的数学思想.

练习册系列答案
相关题目
17.给出以下四个命题:
①若x2+y2=0,则x=y=0
②“若a,b都是偶数,则a+b是偶数”的逆否命题
③“若x=2,则x2-3x+2=0”的逆命题
④“若两个三角形全等,则这两个三角形的面积相等”的否命题
其中真命题的序号是( )
①若x2+y2=0,则x=y=0
②“若a,b都是偶数,则a+b是偶数”的逆否命题
③“若x=2,则x2-3x+2=0”的逆命题
④“若两个三角形全等,则这两个三角形的面积相等”的否命题
其中真命题的序号是( )
| A. | ① | B. | ①②③④ | C. | ①②③ | D. | ①② |
12.已知函数f(x)=3tanωx+1,若对任意x1,x2∈(-$\frac{π}{3}$,$\frac{π}{4}$)且x1≠x2,均有[f(x1)-f(x2)](x1-x2)<0成立.则实数ω的取值范围是( )
| A. | -$\frac{3}{2}$≤ω≤$\frac{3}{2}$ | B. | -$\frac{3}{2}$≤ω≤0 | C. | -2≤ω<0 | D. | -2≤ω≤2 |
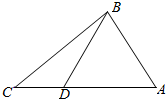 如图,在△ABC中,sin$\frac{∠ABC}{2}$=$\frac{\sqrt{3}}{3}$,AB=2,点D在线段AC上,且AD=2DC,BD=$\frac{4\sqrt{3}}{3}$.
如图,在△ABC中,sin$\frac{∠ABC}{2}$=$\frac{\sqrt{3}}{3}$,AB=2,点D在线段AC上,且AD=2DC,BD=$\frac{4\sqrt{3}}{3}$.