题目内容
若周期函数f(x)是定义在R上的奇函数,且f(x)的最小正周期为3,f(1)<2,f(2)=
则m的取值范围为
| 1 |
| m |
m<-
或m>0
| 1 |
| 2 |
m<-
或m>0
.| 1 |
| 2 |
分析:根据f(x)为奇函数且周期为3,得到f(2)=
=-f(1),再根据f(1)的范围求出m的取值范围.
| 1 |
| m |
解答:解:∵f(x)是定义在R上的奇函数,且f(x)的最小正周期为3
∴f(2)=f(2-3)=-f(1)=
由于f(1)<2,故f(2)=
>-2,解得m<-
或m>0
故答案为:m<-
或m>0
∴f(2)=f(2-3)=-f(1)=
| 1 |
| m |
由于f(1)<2,故f(2)=
| 1 |
| m |
| 1 |
| 2 |
故答案为:m<-
| 1 |
| 2 |
点评:本题考查了抽象函数的周期性和奇偶性,属于基础题型.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 则m的取值范围为________.
则m的取值范围为________.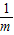 则m的取值范围为 .
则m的取值范围为 .