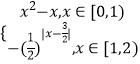题目内容
【题目】已知函数![]() (
(![]() ,
, ![]() ,
, ![]() ),
),![]() 是自然对数的底数.
是自然对数的底数.
(Ⅰ)当![]() ,
, ![]() 时,求函数
时,求函数![]() 的零点个数;
的零点个数;
(Ⅱ)若![]() ,求
,求![]() 在
在![]() 上的最大值.
上的最大值.
【答案】(Ⅰ)2;(Ⅱ)见解析.
【解析】试题分析:(Ⅰ) ![]() ,
, ![]() ,由导数性质得
,由导数性质得![]() 是(0,+∞)上的增函数,是(-∞,0)上的减函数,由此能求出f(x)的零点个数.
是(0,+∞)上的增函数,是(-∞,0)上的减函数,由此能求出f(x)的零点个数.
(Ⅱ)当x∈[-1,1]时, ![]()
![]() ,由导数性质得f(x)是[-1,0]上的减函数,[0,1]上的增函数,由此利用导数性质和构造法能求出a的取值范围.
,由导数性质得f(x)是[-1,0]上的减函数,[0,1]上的增函数,由此利用导数性质和构造法能求出a的取值范围.
试题解析:
(Ⅰ)![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
当![]() 时,
时, ![]() ,∴
,∴![]() ,故
,故![]() 是
是![]() 上的增函数,
上的增函数,
当![]() 时,
时, ![]() ,∴
,∴![]() ,故
,故![]() 是
是![]() 上的减函数,
上的减函数,
![]() ,
, ![]() ,∴存在
,∴存在![]() 是
是![]() 在
在![]() 上的唯一零点;
上的唯一零点;
![]() ,
, ![]() ,∴存在
,∴存在![]() 是
是![]() 在
在![]() 上的唯一零点,
上的唯一零点,
所以![]() 的零点个数为2.
的零点个数为2.
(Ⅱ)![]()
![]() ,
,
当![]() 时,由
时,由![]() ,可知
,可知![]() ,
, ![]() ,∴
,∴![]() ,
,
当![]() 时,由
时,由![]() ,可知
,可知![]() ,
, ![]() ,∴
,∴![]() ,
,
当![]() 时,
时, ![]() ,
,
∴![]() 是
是![]() 上的减函数,
上的减函数, ![]() 上的增函数,
上的增函数,
∴当![]() 时,
时, ![]() ,
, ![]() 为
为![]() 和
和![]() 中的较大者.
中的较大者.
而![]() ,设
,设![]() (
(![]() ),
),
∵![]()
![]() (当且仅当
(当且仅当![]() 时等号成立),
时等号成立),
∴![]() 在
在![]() 上单调递增,而
上单调递增,而![]() ,
,
∴当![]() 时,
时, ![]() ,即
,即![]() 时,
时, ![]() ,∴
,∴![]() .
.
∴![]() 在
在![]() 上的最大值为
上的最大值为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目