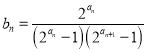题目内容
【题目】定义域为R的函数f(x)满足f(x+2)=2f(x),当x∈[0,2)时,f(x)= 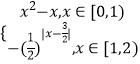 ,若x∈[﹣4,﹣2)时,f(x)≥
,若x∈[﹣4,﹣2)时,f(x)≥ ![]() 恒成立,则实数t的取值范围是( )
恒成立,则实数t的取值范围是( )
A.[﹣2,0)∪(0,1)
B.[﹣2,0)∪[1,+∞)
C.[﹣2,1]
D.(﹣∞,﹣2]∪(0,1]
【答案】D
【解析】解:当x∈[0,1)时,f(x)=x2﹣x∈[﹣ ![]() ,0]
,0]
当x∈[1,2)时,f(x)=﹣(0.5)|x﹣1.5|∈[﹣1, ![]() ]
]
∴当x∈[0,2)时,f(x)的最小值为﹣1
又∵函数f(x)满足f(x+2)=2f(x),
当x∈[﹣2,0)时,f(x)的最小值为﹣ ![]()
当x∈[﹣4,﹣2)时,f(x)的最小值为﹣ ![]()
若x∈[﹣4,﹣2)时, ![]() 恒成立,
恒成立,
∴ ![]()
即 ![]()
即4t(t+2)(t﹣1)≤0且t≠0
解得:t∈(﹣∞,﹣2]∪(0,l]
故选D

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目