题目内容
三角形三内角的大小成等差数列,如果最小角为450,最小边长为
,那么最大边的长为( )
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
分析:根据三角形的三个内角成等差数列,最小的角为45°,设出等差数列的公差为d,表示出其他的两角,根据内角和定理列出关于d的方程,求出方程的解即可得到d的值,根据大边对大角,求出最大角的度数,然后利用正弦定理即可求出最长边.
解答:解:三角形三内角的大小成等差数列设公差为d,最小角为45°,
则中间的角为45°+d,最大的角为45°+2d,
所以45°+(45°+d)+(45°+2d)=180°,解得d=15°,
则此三角形的三个内角分别为45°,60°,75°,又最小的边为
,
设最大的边为x,
因为sin75°=sin(45°+30°)=sin45°cos30°+cos45°sin30°=
,
则根据正弦定理得
=
,解得x=
(
+
).
故选B
则中间的角为45°+d,最大的角为45°+2d,
所以45°+(45°+d)+(45°+2d)=180°,解得d=15°,
则此三角形的三个内角分别为45°,60°,75°,又最小的边为
| 2 |
设最大的边为x,
因为sin75°=sin(45°+30°)=sin45°cos30°+cos45°sin30°=
| ||||
| 4 |
则根据正弦定理得
| ||
| sin45° |
| x |
| sin75° |
| 1 |
| 2 |
| 6 |
| 2 |
故选B
点评:此题考查学生掌握等差数列的性质,灵活运用正弦定理化简求值,是一道中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 求角A,B,C的大小,又已知顶点C的对边c上的高等于
求角A,B,C的大小,又已知顶点C的对边c上的高等于 ,求三角形各边a,b,c的长.(提示:必要时可验证
,求三角形各边a,b,c的长.(提示:必要时可验证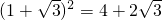 )
)