题目内容
1.已知函数y=f(x)是定义在R上的奇函数,且当x∈(-∞,0)时,不等式f(x)+xf′(x)<0恒成立,若a=30.3f(30.3),b=(logπ3)f(logπ3),c=(${log}_{3}\frac{1}{3}$)f(${log}_{3}\frac{1}{3}$),则a,b,c的大小关系(用“>”连接)是a>c>b.分析 利用导数研究函数的单调性,利用单调性判断a、b、c的大小.
解答 解:函数y=f(x)是定义在R上的奇函数,且当x∈(-∞,0)时,不等式f(x)+xf′(x)<0恒成立,
即xf(x)的导数小于零恒成立,故函数y=xf(x)在(-∞,0)上单调递减,
故 y=xf(x)是偶函数,且它在(0,+∞)上单调递增.
∵30.3>1>logπ3>0>${log}_{3}\frac{1}{3}$=-1,
∵a=30.3f(30.3),b=(logπ3)f(logπ3),c=(${log}_{3}\frac{1}{3}$)f(${log}_{3}\frac{1}{3}$)=-f(-1)=1•f(1),
∴a>c>b,
故答案为:a>c>b.
点评 本题主要考查利用导数研究函数的单调性,利用单调性比较几个数的大小,属于中档题.

练习册系列答案
相关题目
12.若i是虚数单位,复数$\frac{1-2i}{i}$的虚部为( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
16.已知三条不重合的直线m,n,l和两个不重合的平面α,β,下列命题正确的是( )
| A. | 若m∥n,n?α,则m∥α | B. | 若l∥n,m⊥n,则l∥m | ||
| C. | 若l⊥α,m⊥β,且l⊥m,则α⊥β | D. | 若α⊥β,α∩β=m,且m⊥n,则n⊥α |

 如图所示,在等腰梯形ABCD中,AD∥BC,AD=CD=AB=2,∠ABC=60°,将三角形ABD沿BD折起,使点A在平面BCD上的投影G落在BD上.
如图所示,在等腰梯形ABCD中,AD∥BC,AD=CD=AB=2,∠ABC=60°,将三角形ABD沿BD折起,使点A在平面BCD上的投影G落在BD上.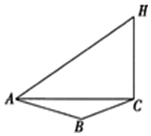 某烟花厂家为了测试最新研制出的一种“冲天”产品升空的安全性,特对其进行了一项测试.如图,这种烟花在燃放点C进行燃放实验,测试人员甲、乙分别在A,B两地(假设三地在同一水平面上),测试人员甲测得A、B两地相距80米且∠BAC=60°,甲听到烟花燃放“冲天”时的声音的时间比乙晚$\frac{1}{17}$秒.在A地测得该烟花升至最高点H处的仰角为60°.(已知声音的传播速度为340米∕秒)
某烟花厂家为了测试最新研制出的一种“冲天”产品升空的安全性,特对其进行了一项测试.如图,这种烟花在燃放点C进行燃放实验,测试人员甲、乙分别在A,B两地(假设三地在同一水平面上),测试人员甲测得A、B两地相距80米且∠BAC=60°,甲听到烟花燃放“冲天”时的声音的时间比乙晚$\frac{1}{17}$秒.在A地测得该烟花升至最高点H处的仰角为60°.(已知声音的传播速度为340米∕秒)