题目内容
已知a2+b2+c2=1,若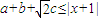 对任意实数a,b,c恒成立,求实数x的取值范围.
对任意实数a,b,c恒成立,求实数x的取值范围.
【答案】分析:由柯西不等式,我们易结合a2+b2+c2=1,得到 ≤(1+1+2)(a2+b2+c2)=4,再由
≤(1+1+2)(a2+b2+c2)=4,再由 对任意实数a,b,c恒成立,故
对任意实数a,b,c恒成立,故 =2,解绝对值不等式,即可得到答案.
=2,解绝对值不等式,即可得到答案.
解答:解:∵ ≤(1+1+2)(a2+b2+c2)=4
≤(1+1+2)(a2+b2+c2)=4
∴ ≤2(5分)
≤2(5分)
又∵ 对任意实数a,b,c恒成立,
对任意实数a,b,c恒成立,
∴ =2
=2
解得x≤-3或x≥1(10分)
点评:该题考查柯西不等式、绝对值不等式求解;是容易题.
 ≤(1+1+2)(a2+b2+c2)=4,再由
≤(1+1+2)(a2+b2+c2)=4,再由 对任意实数a,b,c恒成立,故
对任意实数a,b,c恒成立,故 =2,解绝对值不等式,即可得到答案.
=2,解绝对值不等式,即可得到答案.解答:解:∵
 ≤(1+1+2)(a2+b2+c2)=4
≤(1+1+2)(a2+b2+c2)=4∴
 ≤2(5分)
≤2(5分)又∵
 对任意实数a,b,c恒成立,
对任意实数a,b,c恒成立,∴
 =2
=2解得x≤-3或x≥1(10分)
点评:该题考查柯西不等式、绝对值不等式求解;是容易题.

练习册系列答案
相关题目
△ABC中,角A、B、C的对边分别为a、b、c,已知a2=b2+c2+bc,则角A等于( )
| A、30° | B、45° | C、60° | D、120° |