题目内容
设椭圆E：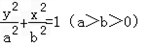
的上焦点是F1，过点P（3，4）和F1作直线PF1交椭圆于A、B两点，已知A（
）．
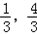（1）求椭圆E的方程；
（2）设点C是椭圆E上到直线PF1距离最远的点，求C点的坐标．
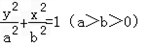的上焦点是F1，过点P（3，4）和F1作直线PF1交椭圆于A、B两点，已知A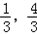（）．（1）求椭圆E的方程；
（2）设点C是椭圆E上到直线PF1距离最远的点，求C点的坐标．
解：（1）由A（
）和P（3，4）得直线PF1的方程为：y=x+1
令x=0，得y=1，即c=1
椭圆E的焦点为F1（0，1）、F2（0，﹣1），
由椭圆的定义可知
∴
椭圆E的方程为
（2）设与直线PF1平行的直线l：y=x+m，
由
，消去y得3x2+2mx+m2﹣2=0
△=（2m）2﹣4×3×（m2﹣2）=0，即
要使点C到直线PF1的距离最远，则直线L要在直线PF1的下方，所以
此时直线l与椭圆E的切点坐标为
，
故C
为所求．
）和P（3，4）得直线PF1的方程为：y=x+1令x=0，得y=1，即c=1
椭圆E的焦点为F1（0，1）、F2（0，﹣1），
由椭圆的定义可知
∴
椭圆E的方程为（2）设与直线PF1平行的直线l：y=x+m，
由
，消去y得3x2+2mx+m2﹣2=0△=（2m）2﹣4×3×（m2﹣2）=0，即
要使点C到直线PF1的距离最远，则直线L要在直线PF1的下方，所以
此时直线l与椭圆E的切点坐标为
，故C
为所求． 
练习册系列答案
相关题目
的上焦点是F1，过点P(3，4)和F1作直线PF1交椭圆于A、B两点，若A(
)．
的上焦点是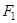
，过点P（3，4）和
).
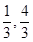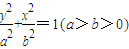的上焦点是F1，过点P（3，4）和F1作直线PF1交椭圆于A、B两点，已知A（
）．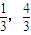