题目内容
（本小题满分12分）
设椭圆E：
的上焦点是
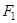，过点P（3，4）和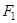作直线P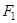交椭圆于A、B两点，已知A(
).
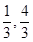(1)求椭圆E的方程；
(2)设点C是椭圆E上到直线P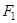距离最远的点，求C点的坐标。
【答案】
19
（1）由A（
）和P（3，4）可求直线
的方程为：y=x+1…………………………1分
令x=0，得y=1,即c=1 …………………………2分
椭圆E的焦点为
、
，由椭圆的定义可知
…………………………4分
∴
…………………………5分
椭圆E的方程为
…………………………6分
（2）设与直线平行的直线
:
…………………………7分
，消去y得
………………………… 8分
，即
…………………………9分
要使点C到直线的距离最远，则直线L要在直线的下方，所以
……………10分
此时直线与椭圆E的切点坐标为
，故C（为所求。 ……………12分
【解析】略
练习册系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
