题目内容
设椭圆E: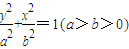 的上焦点是F1,过点P(3,4)和F1作直线PF1交椭圆于A、B两点,已知A(
的上焦点是F1,过点P(3,4)和F1作直线PF1交椭圆于A、B两点,已知A(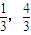 ).
).(1)求椭圆E的方程;
(2)设点C是椭圆E上到直线PF1距离最远的点,求C点的坐标.
【答案】分析:(1)由A(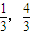 )和P(3,4)能求出直线PF1的方程为:y=x+1,令x=0,得椭圆E的焦点为F1(0,1)、F2(0,-1),由椭圆的定义能求出椭圆E的方程.
)和P(3,4)能求出直线PF1的方程为:y=x+1,令x=0,得椭圆E的焦点为F1(0,1)、F2(0,-1),由椭圆的定义能求出椭圆E的方程.
(2)设与直线PF1平行的直线l:y=x+m,由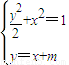 ,得3x2+2mx+m2-2=0,再由根的判别式结合题设条件,能求出C点的坐标..
,得3x2+2mx+m2-2=0,再由根的判别式结合题设条件,能求出C点的坐标..
解答:解:(1)由A(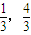 )和P(3,4)得直线PF1的方程为:y=x+1…(1分)
)和P(3,4)得直线PF1的方程为:y=x+1…(1分)
令x=0,得y=1,即c=1 …(2分)
椭圆E的焦点为F1(0,1)、F2(0,-1),
由椭圆的定义可知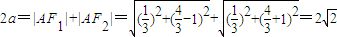 …(4分)
…(4分)
∴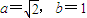 …(5分)
…(5分)
椭圆E的方程为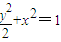 …(6分)
…(6分)
(2)设与直线PF1平行的直线l:y=x+m…(7分),
由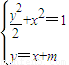 ,消去y得3x2+2mx+m2-2=0…(8分)
,消去y得3x2+2mx+m2-2=0…(8分)
△=(2m)2-4×3×(m2-2)=0,
即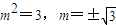 …(9分)
…(9分)
要使点C到直线PF1的距离最远,
则直线L要在直线PF1的下方,所以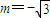 …(10分)
…(10分)
此时直线l与椭圆E的切点坐标为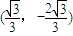 ,
,
故C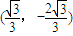 为所求. …(12分)
为所求. …(12分)
点评:本题考查椭圆方程的求法和求点的坐标,具体涉及到椭圆的定义、直线方程的求法、椭圆的简单性质、根的判别式、直线与椭圆的位置关系等基本知识,解题时要认真审题,仔细解答.
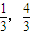 )和P(3,4)能求出直线PF1的方程为:y=x+1,令x=0,得椭圆E的焦点为F1(0,1)、F2(0,-1),由椭圆的定义能求出椭圆E的方程.
)和P(3,4)能求出直线PF1的方程为:y=x+1,令x=0,得椭圆E的焦点为F1(0,1)、F2(0,-1),由椭圆的定义能求出椭圆E的方程.(2)设与直线PF1平行的直线l:y=x+m,由
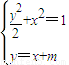 ,得3x2+2mx+m2-2=0,再由根的判别式结合题设条件,能求出C点的坐标..
,得3x2+2mx+m2-2=0,再由根的判别式结合题设条件,能求出C点的坐标..解答:解:(1)由A(
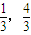 )和P(3,4)得直线PF1的方程为:y=x+1…(1分)
)和P(3,4)得直线PF1的方程为:y=x+1…(1分)令x=0,得y=1,即c=1 …(2分)
椭圆E的焦点为F1(0,1)、F2(0,-1),
由椭圆的定义可知
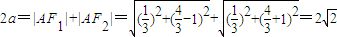 …(4分)
…(4分)∴
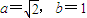 …(5分)
…(5分)椭圆E的方程为
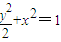 …(6分)
…(6分)(2)设与直线PF1平行的直线l:y=x+m…(7分),
由
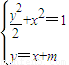 ,消去y得3x2+2mx+m2-2=0…(8分)
,消去y得3x2+2mx+m2-2=0…(8分)△=(2m)2-4×3×(m2-2)=0,
即
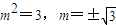 …(9分)
…(9分)要使点C到直线PF1的距离最远,
则直线L要在直线PF1的下方,所以
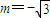 …(10分)
…(10分)此时直线l与椭圆E的切点坐标为
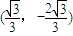 ,
,故C
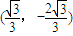 为所求. …(12分)
为所求. …(12分)点评:本题考查椭圆方程的求法和求点的坐标,具体涉及到椭圆的定义、直线方程的求法、椭圆的简单性质、根的判别式、直线与椭圆的位置关系等基本知识,解题时要认真审题,仔细解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的上焦点是
的上焦点是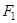 ,过点P(3,4)和
,过点P(3,4)和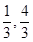 ).
).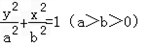 的上焦点是F1,过点P(3,4)和F1作直线PF1交椭圆于A、B两点,已知A(
的上焦点是F1,过点P(3,4)和F1作直线PF1交椭圆于A、B两点,已知A(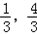 ).
).