题目内容
如图,在由二项式系数所构成的杨辉三角形中,
若第 行中从左至右第
行中从左至右第 与第
与第 个数的比为
个数的比为 ,
,
则 的值为
的值为

若第
 行中从左至右第
行中从左至右第 与第
与第 个数的比为
个数的比为 ,
,则
 的值为
的值为
A.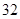 | B.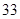 |
C. | D. |
C
试题分析:根据题意,由于由二项式系数所构成的杨辉三角形中,若第
 行中从左至右第
行中从左至右第 与第
与第 个数的比为
个数的比为 ,即可知为
,即可知为 ,则根据组合数的公式可知解得为n=34,g故答案为C.
,则根据组合数的公式可知解得为n=34,g故答案为C.点评:主要是考查了归纳猜想的运用,属于基础题。

练习册系列答案
相关题目
题目内容
 行中从左至右第
行中从左至右第 与第
与第 个数的比为
个数的比为 ,
, 的值为
的值为
A.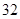 | B.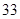 |
C. | D. |
 行中从左至右第
行中从左至右第 与第
与第 个数的比为
个数的比为 ,即可知为
,即可知为 ,则根据组合数的公式可知解得为n=34,g故答案为C.
,则根据组合数的公式可知解得为n=34,g故答案为C.