题目内容
双曲线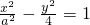
的左、右焦点分别为F1、F2，P是双曲线上一点，PF1的中点在y轴上，线段PF2的长为
，则双曲线的实轴长为
- A.
- B.
- C.3
- D.6
D
分析：由PF1的中点在y轴上知P与F1横坐标相反，PF2⊥x轴，由双曲线的定义求出PF1的长，直角三角形PF1F2中，由勾股定理求半长轴a，从而得到长轴的长．
解答：由题意知，F1（-c，0）、F2（c，0），∵PF1的中点在y轴上，∴P的横坐标为c，PF2⊥x轴，
由双曲线的定义知，PF1-PF2=2a，∴PF1=PF2+2a=+2a，
直角三角形PF1F2中，由勾股定理得：（2c）2+
=
，把c2=a2+4代入可得：
a=3，∴长轴 2a=6；
故答案为D．
点评：本题考查双曲线的性质．
分析：由PF1的中点在y轴上知P与F1横坐标相反，PF2⊥x轴，由双曲线的定义求出PF1的长，直角三角形PF1F2中，由勾股定理求半长轴a，从而得到长轴的长．
解答：由题意知，F1（-c，0）、F2（c，0），∵PF1的中点在y轴上，∴P的横坐标为c，PF2⊥x轴，
由双曲线的定义知，PF1-PF2=2a，∴PF1=PF2+2a=
+2a，直角三角形PF1F2中，由勾股定理得：（2c）2+
=，把c2=a2+4代入可得：a=3，∴长轴 2a=6；
故答案为D．
点评：本题考查双曲线的性质．
练习册系列答案
相关题目
（2011•天津模拟）如图，椭圆
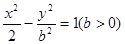的左、右焦点分别是
、
，其一条渐近线方程为
，点
在双曲线上.则
·
＝
的左、右焦点分别是
、
，其一条渐近线方程为
，点
在双曲线上.则
·
＝( )
的左、右焦点分别是
、
，其一条渐近线方程为
，点
在双曲线上.则
·
＝
的左、右焦点分别是
、
，其一条渐近线方程为
，点
在双曲线上.则
·
＝