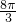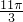题目内容
半径为1的球内切于一个圆锥，已知圆锥的母线与底面的夹角为60°，求证：
(1)圆锥母线长与底面半径之和等于
；
(2)圆锥全面积等于9π．
答案：
解析：
解析：
|
证明：作如下图所示的轴截面图(过球心与圆锥顶点的截面)．
(1)设圆锥的底面半径为r，母线长为l， ∵D、E为切点，OD⊥BC，OE⊥AC， 且OD＝OE＝1，DC＝r，∠DCO＝30°， ∴r＝ 又∠AEO＝∠OEC＝90°， ∴O、D、C、E四点共圆． ∴∠AOE＝∠DCE＝60°． 在Rt△AOE中，AE＝tan60°，即l－r＝tan60°， 故l＝ ∴l＋r＝ (2)S圆锥全＝πr2＋πrl＝9π． |
．
．
．
练习册系列答案
阅读快车系列答案
相关题目
（2012•北海一模）如图，在120°二面角α-l-β内半径为1的圆O1与半径为2的圆O2分别在半平面α、β内，且与棱l切于同一点P，则以圆O1与圆O2为截面的球的表面积为（ ）
