题目内容
半径为1的球内切于一圆锥,则圆锥体积的最小值为
- A.2π
- B.
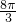
- C.3π
- D.
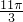
B
分析:设母线与底面的夹角2α,底面半径R,内切球半径r=1,圆锥的高h用α表示R,h,求出圆锥的体积V的表达式,利用基本不等式求出V最小.
解答:设母线与底面的夹角2α,底面半径R,内切球半径r=1,圆锥的高h 则:R=r•cotα=cotα,h=R•tan2α=cotα•tan2α=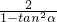 ,
,
圆锥的体积V=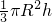 =
=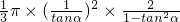
=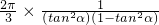 ,
,
而2α<90°,α<45°,所以:tanα<1,1-tan2α>0 又因为:tan2α+(1-tan2α)=1=定值
所以:当tan2α=1-tan2α,即tanα= 时,V最小=
时,V最小=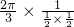 =
=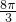 .
.
故选B.
点评:本题考查球与圆锥的位置关系,几何体的体积的求法,基本不等式的应用,考查空间想象能力计算能力.
分析:设母线与底面的夹角2α,底面半径R,内切球半径r=1,圆锥的高h用α表示R,h,求出圆锥的体积V的表达式,利用基本不等式求出V最小.
解答:设母线与底面的夹角2α,底面半径R,内切球半径r=1,圆锥的高h 则:R=r•cotα=cotα,h=R•tan2α=cotα•tan2α=
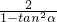 ,
,圆锥的体积V=
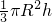 =
=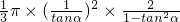
=
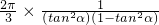 ,
,而2α<90°,α<45°,所以:tanα<1,1-tan2α>0 又因为:tan2α+(1-tan2α)=1=定值
所以:当tan2α=1-tan2α,即tanα=
 时,V最小=
时,V最小=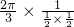 =
=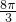 .
.故选B.
点评:本题考查球与圆锥的位置关系,几何体的体积的求法,基本不等式的应用,考查空间想象能力计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•北海一模)如图,在120°二面角α-l-β内半径为1的圆O1与半径为2的圆O2分别在半平面α、β内,且与棱l切于同一点P,则以圆O1与圆O2为截面的球的表面积为( )
(2012•北海一模)如图,在120°二面角α-l-β内半径为1的圆O1与半径为2的圆O2分别在半平面α、β内,且与棱l切于同一点P,则以圆O1与圆O2为截面的球的表面积为( )
