题目内容
4．设Sn为等差数列{an}的前n项和，已知a1-a5+a9=6，则S9的值为（ ）| A． | 54 | B． | 45 | C． | 27 | D． | 18 |
分析 由题意和等差数列的性质求出a5，由等差数列的前n项和公式和性质求出S9的值．
解答 解：在等差数列{an}中，a1-a5+a9=6，
又a1+a9=2a5，则代入得a5=6，
所以${S}_{9}=\frac{9（{a}_{1}+{a}_{9}）}{2}=9{a}_{5}$=54，
故选：A．
点评 本题考查等差数列的前n项和公式，以及等差数列的性质的灵活应用，考查了化简、变形能力．
练习册系列答案
相关题目
9．为了解1500名学生对学校教改试验的意见，打算从中抽取一个容量为50的样本，考虑采用系统抽样，则分段的间隔k为（ ）
| A． | 40 | B． | 30 | C． | 20 | D． | 12 |
16．
随着人们经济收入的不断增长，个人购买家庭轿车已不再是一种时尚．车的使用费用，尤其是随着使用年限的增多，所支出的费用到底会增长多少，一直是购车一族非常关心的问题．某汽车销售公司作了一次抽样调查，并统计得出某款车的使用年限x与所支出的总费用y（万元）有如表的数据资料：
（1）在给出的坐标系中做出散点图；
（2）求线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中的$\widehat{a}$、$\widehat{b}$；
（3）估计使用年限为12年时，车的使用总费用是多少？
（最小二乘法求线性回归方程系数公式$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$）．
随着人们经济收入的不断增长，个人购买家庭轿车已不再是一种时尚．车的使用费用，尤其是随着使用年限的增多，所支出的费用到底会增长多少，一直是购车一族非常关心的问题．某汽车销售公司作了一次抽样调查，并统计得出某款车的使用年限x与所支出的总费用y（万元）有如表的数据资料：| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 总费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
（2）求线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中的$\widehat{a}$、$\widehat{b}$；
（3）估计使用年限为12年时，车的使用总费用是多少？
（最小二乘法求线性回归方程系数公式$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$）．
13．正项等比数列{an}中的a1、a11是函数f（x）=$\frac{1}{3}$x3-4x2+6x-3的极值点，则log${\;}_{\sqrt{6}}}$a5a6=（ ）
| A． | 1 | B． | 2 | C． | $\sqrt{2}$ | D． | -1 |
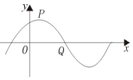已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜$\frac{π}{2}$）的部分图象如图所示，其中点P（1，2）为函数图象的一个最高点，Q（4，0）为函数图象与x轴的一个交点，O为坐标原点．