题目内容
设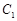 是以
是以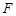 为焦点的抛物线
为焦点的抛物线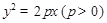 ,
,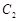 是以直线
是以直线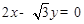 与
与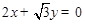 为渐近线,以
为渐近线,以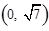 为一个焦点的双曲线.
为一个焦点的双曲线.
(1)求双曲线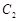 的标准方程;
的标准方程;
(2)若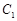 与
与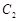 在第一象限内有两个公共点
在第一象限内有两个公共点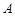 和
和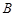 ,求
,求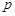 的取值范围,并求
的取值范围,并求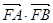 的最大值;
的最大值;
(3)若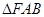 的面积
的面积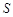 满足
满足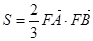 ,求
,求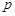 的值.
的值.
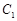 是以
是以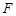 为焦点的抛物线
为焦点的抛物线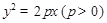 ,
,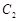 是以直线
是以直线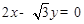 与
与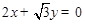 为渐近线,以
为渐近线,以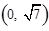 为一个焦点的双曲线.
为一个焦点的双曲线.(1)求双曲线
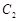 的标准方程;
的标准方程;(2)若
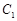 与
与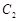 在第一象限内有两个公共点
在第一象限内有两个公共点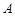 和
和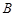 ,求
,求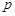 的取值范围,并求
的取值范围,并求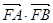 的最大值;
的最大值;(3)若
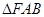 的面积
的面积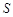 满足
满足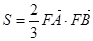 ,求
,求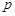 的值.
的值.
(1)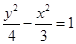 (2)当且仅当
(2)当且仅当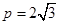 时
时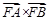 的最大值为9(3)
的最大值为9(3)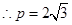
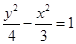 (2)当且仅当
(2)当且仅当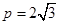 时
时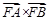 的最大值为9(3)
的最大值为9(3)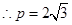
(1)注意焦点在y轴上,并且由渐近线方程可得到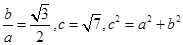 ,可求出a,b值,写出双曲线的标准方程.
,可求出a,b值,写出双曲线的标准方程.
(II)将抛物线方程与双曲线方程联立消y之后得到关于x的一元二次方程,然后利用此方程有两个不同的正实根,确定出p的取值范围,然后再把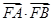 用坐标表示出来,再利用韦达定理转化为关于p的函数,再研究其最值即可.
用坐标表示出来,再利用韦达定理转化为关于p的函数,再研究其最值即可.
(III)先把面积表示出来,在(II)的基础上,先求出|AB|的长度,再根据点到直线的距离公式求出高,最后把S表示成关于p的函数,根据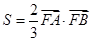 可建立p的方程,解出p的值.
可建立p的方程,解出p的值.
(1)设双曲线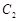 的标准方程为:
的标准方程为: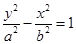 则据题得:
则据题得: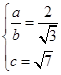
又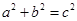

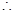 双曲线
双曲线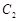 的标准方程为:
的标准方程为: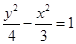
(2)将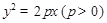 代入到
代入到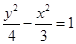 中并整理得:
中并整理得:
设 则
则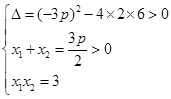
 又
又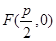

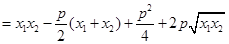

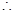 当且仅当
当且仅当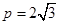 时
时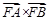 的最大值为9
的最大值为9
(3)直线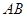 的方程为:
的方程为: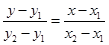 即
即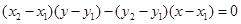
 到直线
到直线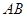 的距离为:
的距离为: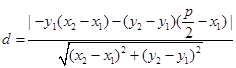
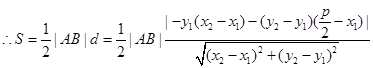

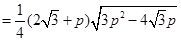
又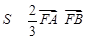

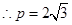
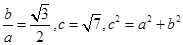 ,可求出a,b值,写出双曲线的标准方程.
,可求出a,b值,写出双曲线的标准方程.(II)将抛物线方程与双曲线方程联立消y之后得到关于x的一元二次方程,然后利用此方程有两个不同的正实根,确定出p的取值范围,然后再把
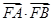 用坐标表示出来,再利用韦达定理转化为关于p的函数,再研究其最值即可.
用坐标表示出来,再利用韦达定理转化为关于p的函数,再研究其最值即可.(III)先把面积表示出来,在(II)的基础上,先求出|AB|的长度,再根据点到直线的距离公式求出高,最后把S表示成关于p的函数,根据
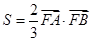 可建立p的方程,解出p的值.
可建立p的方程,解出p的值.(1)设双曲线
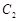 的标准方程为:
的标准方程为: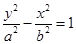 则据题得:
则据题得: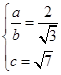
又
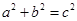

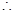 双曲线
双曲线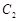 的标准方程为:
的标准方程为: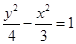
(2)将
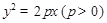 代入到
代入到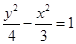 中并整理得:
中并整理得:
设
 则
则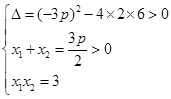
 又
又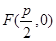

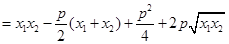

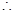 当且仅当
当且仅当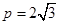 时
时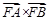 的最大值为9
的最大值为9(3)直线
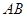 的方程为:
的方程为: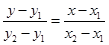 即
即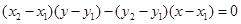
 到直线
到直线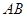 的距离为:
的距离为: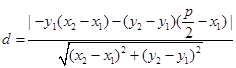
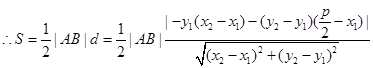

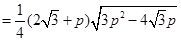
又


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, 中,
中,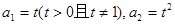 ,且
,且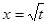 是函数
是函数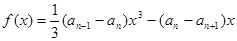 的一个极值点.
的一个极值点.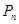 的坐标为(1,
的坐标为(1,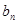 )(
)(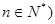 ,过函数
,过函数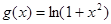 图像上的点
图像上的点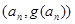 的切线始终与
的切线始终与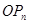 平行(O 为原点),求证:当
平行(O 为原点),求证:当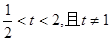 时,不等式
时,不等式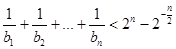 对任意
对任意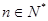 都成立.
都成立.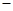 3,0),C(3,0)另两边所在直线的斜率之积为
3,0),C(3,0)另两边所在直线的斜率之积为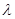 (
(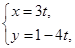 (
(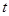 为参数)与圆
为参数)与圆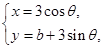 (
(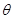 为参数)相切,则
为参数)相切,则 ( )
( )
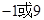
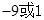
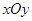 中,设点
中,设点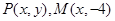 ,坐标原点
,坐标原点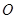 在以线段
在以线段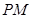 为直径的圆上
为直径的圆上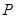 的轨迹C的方程;
的轨迹C的方程;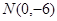 的直线
的直线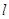 与轨迹C交于两点
与轨迹C交于两点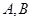 ,点
,点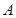 关于
关于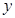 轴的对称点为
轴的对称点为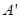 ,试判断直线
,试判断直线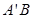 是否恒过一定点,并证明你的结论.
是否恒过一定点,并证明你的结论. 是单位圆
是单位圆 上的任意一点,
上的任意一点, 是过点
是过点 轴垂直的直线,
轴垂直的直线, 是直线
是直线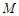 在直线
在直线 . 当点
. 当点 .
. 的直线交曲线
的直线交曲线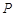 ,
,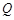 两点,其中
两点,其中 轴上的射影为点
轴上的射影为点 ,直线
,直线 交曲线
交曲线 . 是否存在
. 是否存在 ,使得对任意的
,使得对任意的 ,都有
,都有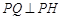 ?若存在,求
?若存在,求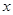 轴的非负半轴为极轴建立极坐标系,曲线E的极坐标方程为
轴的非负半轴为极轴建立极坐标系,曲线E的极坐标方程为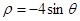 ,曲线F的参数方程为
,曲线F的参数方程为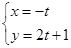 (t为参数)
(t为参数)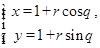 (θ为参数,r >0),若直线l与圆C相切,求r的值.
(θ为参数,r >0),若直线l与圆C相切,求r的值.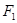 、
、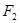 是椭圆
是椭圆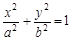
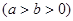 的左、右焦点,
的左、右焦点,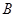 是该椭圆短轴的一个端点,直线
是该椭圆短轴的一个端点,直线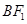 与椭圆
与椭圆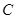 交于点
交于点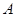 ,若
,若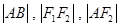 成等差数列,则该椭圆的离心率为 .
成等差数列,则该椭圆的离心率为 .