题目内容
如图,已知直线l1:4x+y=0,直线l2:x+y-1=0以及l2上一点P(3,-2).(Ⅰ)求圆心M在l1上且与直线l2相切于点P的圆⊙的方程.
(Ⅱ)在(Ⅰ)的条件下;若直线l1分别与直线l2、圆⊙依次相交于A、B、C三点,利用代数法验证:|AP|2=|AB|•|AC|.

【答案】分析:(Ⅰ)根据圆心坐标和圆半径能导出b=-4a.设直线l2的斜率k2=-1,过P,C两点的直线斜率kPC,因PC⊥l2,kPC=1,由此可得到所求圆的方程.
(Ⅱ)由题设条件求出A 和圆心M(1,-4),由此能得到|AP|和|AM|,再由|AB|•|AC|=(|AM|-r)(|AM|+r)
和圆心M(1,-4),由此能得到|AP|和|AM|,再由|AB|•|AC|=(|AM|-r)(|AM|+r)
= =|AP|2,化简得证答案.
=|AP|2,化简得证答案.
解答: 解:(Ⅰ)设圆心为M(a,b),半径为r,依题意,
解:(Ⅰ)设圆心为M(a,b),半径为r,依题意,
b=-4a.(2分)
设直线l2的斜率k2=-1,过P,C两点的直线斜率kPC,因PC⊥l2,
故kPC×k2=-1,
∴ ,(4分)
,(4分)
解得a=1,b=-4. .(5分)
.(5分)
所求圆的方程为 .(6分)
.(6分)
(Ⅱ)联立 则A
则A
则 .(8分)
.(8分)
圆心M(1,-4),
|AB|•|AC|=(|AM|-r)(|AM|+r)
=
=|AP|2.(11分)
所以|AP|2=|AB|•|AC|得到证明(12分)
点评:本题主要考查圆的几何性质,直线与圆的位置关系等基础知识,考查解析几何的基本思想方法和基本解题能力.
(Ⅱ)由题设条件求出A
 和圆心M(1,-4),由此能得到|AP|和|AM|,再由|AB|•|AC|=(|AM|-r)(|AM|+r)
和圆心M(1,-4),由此能得到|AP|和|AM|,再由|AB|•|AC|=(|AM|-r)(|AM|+r)=
 =|AP|2,化简得证答案.
=|AP|2,化简得证答案.解答:
 解:(Ⅰ)设圆心为M(a,b),半径为r,依题意,
解:(Ⅰ)设圆心为M(a,b),半径为r,依题意,b=-4a.(2分)
设直线l2的斜率k2=-1,过P,C两点的直线斜率kPC,因PC⊥l2,
故kPC×k2=-1,
∴
 ,(4分)
,(4分)解得a=1,b=-4.
 .(5分)
.(5分)所求圆的方程为
 .(6分)
.(6分)(Ⅱ)联立
 则A
则A
则
 .(8分)
.(8分)圆心M(1,-4),

|AB|•|AC|=(|AM|-r)(|AM|+r)
=

=|AP|2.(11分)
所以|AP|2=|AB|•|AC|得到证明(12分)
点评:本题主要考查圆的几何性质,直线与圆的位置关系等基础知识,考查解析几何的基本思想方法和基本解题能力.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
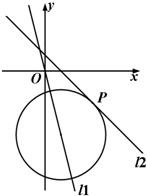 如图,已知直线l1:4x+y=0,直线l2:x+y-1=0以及l2上一点P(3,-2).
如图,已知直线l1:4x+y=0,直线l2:x+y-1=0以及l2上一点P(3,-2).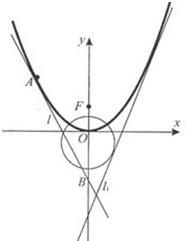 如图,已知直线l1:y=2x+m(m<0)与抛物线C1:y=ax2(a>0)和圆C2:x2+(y+1)2=5都相切,F是C1的焦点.
如图,已知直线l1:y=2x+m(m<0)与抛物线C1:y=ax2(a>0)和圆C2:x2+(y+1)2=5都相切,F是C1的焦点. 如图,已知直线l1:4x+y=0,直线l2:x+y-1=0以及l2上一点P(3,-2).求有圆心在l1上且与直线l2相切于点P的圆的方程.
如图,已知直线l1:4x+y=0,直线l2:x+y-1=0以及l2上一点P(3,-2).求有圆心在l1上且与直线l2相切于点P的圆的方程.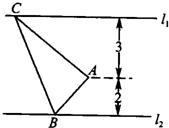 如图,已知直线l1∥l2,点A是l1,l2之间的定点,点A到l1,l2之间的距离分别为3和2,点B是l2上的一动点,作AC⊥AB,且AC与l1交于点C,则△ABC的面积的最小值为
如图,已知直线l1∥l2,点A是l1,l2之间的定点,点A到l1,l2之间的距离分别为3和2,点B是l2上的一动点,作AC⊥AB,且AC与l1交于点C,则△ABC的面积的最小值为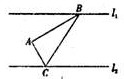 如图,已知直线l1∥l2,点A是l1,l2上两直线之间的动点,且到l1距离为4,到l2距离为3,若
如图,已知直线l1∥l2,点A是l1,l2上两直线之间的动点,且到l1距离为4,到l2距离为3,若