题目内容
函数f(x)=2sinπx与函数f(x)=
的图象所有交点的横坐标之和为( )
| 3 | x-1 |
| A、8 | B、9 | C、16 | D、17 |
考点:函数的零点与方程根的关系,正弦函数的图象
专题:函数的性质及应用
分析:根据函数的对称性,利用数形结合即可得到结论.
解答:
 解:函数f(x)=
解:函数f(x)=
关于点(1,0)对称,而f(x)=2sinπx也关于点(1,0)对称,
由
=2,解得x=9,
由
=-2,解得x=-7,
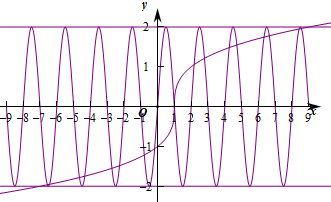
作出两个函数的图象,由图象可知两个图象共有17个交点,除(1,0)外,
其余16个交点分别关于(1,0)对称,
设对称的两个交点的横坐标分别为x1,x2,
则x1+x2=2,
则所有交点的横坐标之和为2×8+1=17,
故选:D
 解:函数f(x)=
解:函数f(x)=| 3 | x-1 |
由
| 3 | x-1 |
由
| 3 | x-1 |
作出两个函数的图象,由图象可知两个图象共有17个交点,除(1,0)外,
其余16个交点分别关于(1,0)对称,
设对称的两个交点的横坐标分别为x1,x2,
则x1+x2=2,
则所有交点的横坐标之和为2×8+1=17,
故选:D
点评:本题主要考查函数零点的应用,根据方程和函数之间的关系,利用数形结合,结合函数的对称性是解决本题的关键.

练习册系列答案
相关题目
若函数f(x)=
在R上为增函数,则实数a的取值范围是( )
|
| A、(0,2] |
| B、(-∞,2) |
| C、(1,2] |
| D、(-∞,2] |
若a,b是任意实数,且a>b,则下列不等式正确的是( )
| A、a2>b2 | ||
B、
| ||
| C、lg(a-b)>0 | ||
| D、b<a |
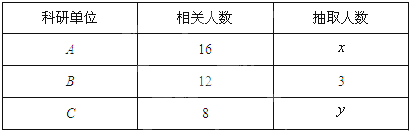
为了对某课题进行研究,用分层抽样方法从三所科研单位A、B、C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人):则( )

| A、x=6,y=4 |
| B、x=4,y=3 |
| C、x=7,y=4 |
| D、x=4,y=2 |
函数y=
在(0,+∞)上( )
| 1 |
| x |
| A、既无最大值又无最小值 |
| B、仅有最小值 |
| C、既有最大值又有最小值 |
| D、仅有最大值 |
下列各式正确的是( )
A、
| |||
B、
| |||
C、
| |||
| D、a0=1 |
已知函数f(x)是偶函数,其图象与x轴有四个不同的交点,则函数f(x-1)的所有零点之和为( )
| A、0 | B、8 | C、4 | D、无法确定 |