题目内容
在梯形ABCD中，∠DAB＝∠ABC＝90°，AD＞BC，P为梯形ABCD所在平面外一点，且PA⊥平面ABCD，M为PB上一点，过M、A、D作截面交PC于N(如图)，判断截面AMND是什么图形?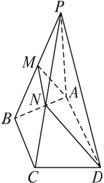
思路解析：利用线面平行，线面垂直的性质.
证明:由已知有AD∥BC，而BC
平面PBC，AD
平面PBC,∴AD∥平面PBC.
又MN为过M、A、D的截面与平面PBC的交线,∴MN∥AD.
又MN＜BC＜AD,∴AMND为梯形.
∵PA⊥平面ABCD，AD
平面ABCD,∴PA⊥AD.
又DA⊥AB，AB∩AP＝A,∴DA⊥平面APB.
∵AM
平面APB,
∴DA⊥AM,故截面AMND为直角梯形.
练习册系列答案
阅读快车系列答案
相关题目
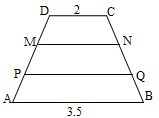如图，在梯形ABCD中，DM=MP=PA，MN∥PQ∥AB，DC=2cm，AB=3.5cm求MN和PQ的长．
如图，已知在梯形ABCD中，AB∥DC，且AB=2CD，E、F分别是DC、AB的中点，设
如图所示，在梯形ABCD中，CD=2，AC=
如图，在梯形ABCD中，AD∥BC，AD⊥AB，AD=1，AB=2，BC=3，P是BC上的一个动点，当