题目内容
11.a,b,c为一个三角形的三边,且s2=2ab,这里s=$\frac{1}{2}$(a+b+c),试证s<2a.分析 由a,b,c为一个三角形的三边,可得a+c>b,s>b,故s2>sb,即2ab>sb,从而证得s<2a.
解答 证明:∵a,b,c为一个三角形的三边,∴a+c>b.
又s=$\frac{1}{2}$(a+b+c),
∴s>b,
∴s2>sb.
又∵s2=2ab,
∴2ab>sb,
∴s<2a.
点评 本题考查三角形的任意两边之和大于第三边,不等式的性质的应用,证得s>b是解题的关键,属于中档题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
19.若x∈C,则关于x的方程x2-5|x|+6=0的所有解的和为( )
| A. | 0 | B. | 5 | C. | 10 | D. | 5i |
20.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}x(0<x<2)}\\{-{x}^{2}+8x-15(x≥2)}\end{array}\right.$,g(x)=kx-2,若方程f(x)=g(x)有三个根,则实数k的取值范围是( )
| A. | (0,$\frac{1}{2}$) | B. | ($\frac{1}{2}$,1) | C. | (-2$\sqrt{13}$+8,1) | D. | ($\frac{1}{2}$,-2$\sqrt{13}$+8) |
1.点A在z轴上,它到点(2$\sqrt{2}$,$\sqrt{5}$,1)的距离是$\sqrt{13}$,则点A的坐标是( )
| A. | (0,0,-1) | B. | (0,1,1) | C. | (0,0,1) | D. | (0,0,13) |
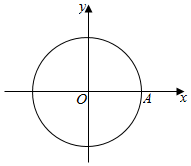 如图,圆周上点A依逆时针方向做匀速圆周运动,已知A点1分钟转过θ(0°<θ<180°),2分钟到第三象限,16分钟后回到原来的位置,求θ.
如图,圆周上点A依逆时针方向做匀速圆周运动,已知A点1分钟转过θ(0°<θ<180°),2分钟到第三象限,16分钟后回到原来的位置,求θ.