题目内容
11.已知函数f(x)=x3+lg($\sqrt{{x}^{2}+1}$+x,若f(x)的定义域中是a,b满足f(-a)+f(-b)=f(a)+f(b)+3,则f(a)+f(b)=-$\frac{3}{2}$.分析 函数的定义域为R,求f(-x)=-x3+(0-lg($\sqrt{{x}^{2}+1}$+x))=-f(x),根据奇函数的性质可得结论.
解答 解:f(x)=x3+lg($\sqrt{{x}^{2}+1}$+x),
∴f(-x)=-x3+(0-lg($\sqrt{{x}^{2}+1}$+x))
=-f(x),
∴f(x)为奇函数,
∵f(-a)+f(-b)=f(a)+f(b)+3,
∴f(a)+f(b)=-$\frac{3}{2}$.
点评 考查了奇函数的判断和对抽象函数的理解.

练习册系列答案
相关题目
2.在复平面内,复数z满足z(1-i)=(1+2i)(i是虚数单位),则z对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
6.已知函数f(x)的对应关系如表:
若函数f(x)不存在反函数,则实数m的取值集合为{-2,1,3,5}.
| x | -2 | -1 | 0 | 1 | 2 |
| f(x) | 3 | -2 | 1 | 5 | m |
16.已知$\overrightarrow{OA}$=(2,3),$\overrightarrow{OB}=(-3,y)$,且$\overrightarrow{OA}⊥\overrightarrow{OB}$,则y等于( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
3.方程9x+|3x+b|=5(b∈R)有两个负实数解,则b的取值范囤为( )
| A. | (3,5) | B. | (-5.25,-5) | C. | [-5.25,-5) | D. | 前三个都不正确 |
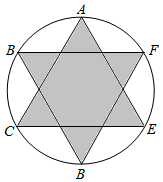 如图,圆周上的6个点是该圆周的6个等分点,分别连接AC,CE,EA,BD,DF,FB,在圆内部随机投掷一点,则该点不落在阴影部分内的概率是1-$\frac{\sqrt{3}}{π}$.
如图,圆周上的6个点是该圆周的6个等分点,分别连接AC,CE,EA,BD,DF,FB,在圆内部随机投掷一点,则该点不落在阴影部分内的概率是1-$\frac{\sqrt{3}}{π}$.