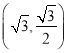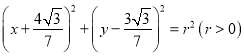题目内容
【题目】已知函数![]()
![]()
(1)当函数![]() 存在零点时,求
存在零点时,求![]() 的取值范围;
的取值范围;
(2)讨论函数![]() 在区间
在区间![]() 内零点的个数.
内零点的个数.
【答案】(1)![]() 或
或![]() (2)当
(2)当![]() ,
,![]() 在区间
在区间![]() 上没有零点;当
上没有零点;当![]() 或
或![]() 时,
时,![]() 在
在![]() 上只有1个零点;当
上只有1个零点;当![]() 时,
时,![]() 在区间
在区间![]() 上有2个零点.
上有2个零点.
【解析】
(1)将问题转化为一元二次方程有根的问题,根据![]() 进行计算;
进行计算;
(2)根据二次函数的对称轴,以及![]() 的正负,结合零点存在定理,对参数
的正负,结合零点存在定理,对参数![]() 进行分类讨论即可.
进行分类讨论即可.
(1)因为函数![]() 有零点,
有零点,
所以方程![]() 有实数根.
有实数根.
所以![]() ,解得
,解得![]() ,或
,或![]()
因此,所求![]() 的取值范围是
的取值范围是![]() ,或
,或![]() .
.
(2)由题意可知![]() 的对称轴为
的对称轴为![]() ,
,
由(1)知:①当![]() 时,
时,![]() ,
,
故![]() 在
在![]() 内没有零点;
内没有零点;
②当![]() 时,对称轴
时,对称轴![]() ,
,
故![]() 在
在![]() 上单调递增.
上单调递增.
又因为![]() ,故
,故![]() 在区间
在区间![]() 恒成立,
恒成立,
故![]() 在区间
在区间![]() 上没有零点;
上没有零点;
③当![]() 时,
时,![]() =
=![]() ,则函数零点为
,则函数零点为![]() ,
,
故![]() 在区间
在区间![]() 上只有一个零点;
上只有一个零点;
④当![]() 时,对称轴
时,对称轴![]() ,且
,且![]() ,
,
又因为![]()
当![]() 时,即
时,即![]() 时,由零点存在定理得
时,由零点存在定理得
函数![]() 在区间
在区间![]() 上只有1个零点,
上只有1个零点,
当![]() ,且
,且![]() ,即
,即![]() 时,
时,
![]() 在
在![]() 上有2个零点,
上有2个零点,
当![]() ,且
,且![]() ,即
,即![]() 且
且![]()
不存在此类情况.
综上所述:
当![]() ,
,![]() 在区间
在区间![]() 上没有零点;
上没有零点;
当![]() 或
或![]() 时,
时,![]() 在
在![]() 上只有1个零点;
上只有1个零点;
当![]() 时,
时,![]() 在区间
在区间![]() 上有2个零点.
上有2个零点.

 阅读快车系列答案
阅读快车系列答案【题目】为预防![]() 病毒爆发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于
病毒爆发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于![]() %,则认为测试没有通过),公司选定
%,则认为测试没有通过),公司选定![]() 个流感样本分成三组,测试结果如下表:
个流感样本分成三组,测试结果如下表:
|
|
| |
疫苗有效 |
|
|
|
疫苗无效 |
|
|
|
已知在全体样本中随机抽取![]() 个,抽到
个,抽到![]() 组疫苗有效的概率是
组疫苗有效的概率是![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)现用分层抽样的方法在全体样本中抽取![]() 个测试结果,问应在
个测试结果,问应在![]() 组抽取多少个?
组抽取多少个?
(Ⅲ)已知![]() ,
,![]() ,求不能通过测试的概率.
,求不能通过测试的概率.
【题目】已知国家某![]() 级大型景区对拥挤等级与每日游客数量
级大型景区对拥挤等级与每日游客数量![]() (单位:百人)的关系有如下规定:当
(单位:百人)的关系有如下规定:当![]() 时,拥挤等级为“优”;当
时,拥挤等级为“优”;当![]() 时,拥挤等级为“良”;当
时,拥挤等级为“良”;当![]() 时,拥挤等级为“拥挤”;当
时,拥挤等级为“拥挤”;当![]() 时,拥挤等级为“严重拥挤”.该景区对6月份的游客数量作出如图的统计数据:
时,拥挤等级为“严重拥挤”.该景区对6月份的游客数量作出如图的统计数据:
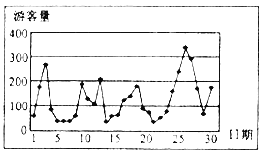
(1)下面是根据统计数据得到的频率分布表,求出![]() 的值,并估计该景区6月份游客人数的平均值(同一组中的数据用该组区间的中点值作代表);
的值,并估计该景区6月份游客人数的平均值(同一组中的数据用该组区间的中点值作代表);
游客数量(单位:百人) |
|
|
|
|
天数 |
| 10 | 4 | 1 |
频率 |
|
|
|
|
(2)某人选择在6月1日至6月5日这5天中任选2天到该景区游玩,求他这2天遇到的游客拥挤等级均为“优”的频率.