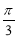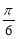题目内容
已知函数y=Asin(ωx+φ) (A>0,ω>0,|φ|<π)的 一段图象如图所示

(1)求函数的解析式;
(2)求这个函数的单调增区间。
(1) (2)
(2)
【解析】
试题分析:(1)由图像的振幅可求 ,由图像可知其周期,再用周期求
,由图像可知其周期,再用周期求 ,最后将图中的一个点代入可求
,最后将图中的一个点代入可求 。(2)将整体角
。(2)将整体角 代入正弦的单调增区间,求
代入正弦的单调增区间,求 的范围及为这个函数的增区间。
的范围及为这个函数的增区间。
试题解析:【解析】
(1)由图可知A=3
T= =π,又
=π,又 ,故ω=2
,故ω=2
所以y=3sin(2x+φ),把 代入得:
代入得:
故 ,∴
,∴ ,k∈Z
,k∈Z
∵|φ|<π,故k=1, ∴
∴
(2)由题知
解得:
故这个函数的单调增区间为
考点:1求三角函数解析式;2正弦的单调区间。

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
研究性学习小组为了解某生活小区居民用水量 (吨)与气温
(吨)与气温 (℃)之间的关系,随机统计并制作了5天该小区居民用水量与当天气温的对应表:
(℃)之间的关系,随机统计并制作了5天该小区居民用水量与当天气温的对应表:
日期 | 9月5日 | 10月3日 | 10月8日 | 11月16日 | 12月21日 |
气温 | 18 | 15 | 11 | 9 | -3 |
用水量 | 57 | 46 | 36 | 37 | 24 |
(1)若从这随机统计的5天中任取2天,求这2天中有且只有1天用水量低于40吨的概率(列出所有的基本事件);
(2)由表中数据求得线性回归方程 中的
中的 ,试求出
,试求出 的值,并预测当地气温为5℃时,该生活小区的用水量.
的值,并预测当地气温为5℃时,该生活小区的用水量.