题目内容
如图
图
思路分析:由BD·CD可联想到割线定理,则BD·CD=DA·DE=DA(AD+AE)=AD2+AD·AE.
只需证AD·AE=AB·AC即可.
事实上,由△ABE∽△ADC易证.
证明:连结BE,
由割线定理,得BD·CD=DA·DE,
∵∠1=∠2,∠2=∠3,∴∠1=∠3.
又∵∠ACD=∠E,∴△ABE∽△ADC.
∴
=
.
∴AB·AC=AD·AE.
∴BD·CD-AB·AC=DA·DE-AD·AE=AD(DE-AE)=AD2.
练习册系列答案
相关题目
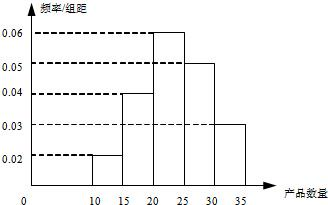为了调查某厂2000名工人生产某种产品的能力，随机抽查了m位工人某天生产该产品的数量，产品数量的分组区间为[10，15），[15，20），[20，25），[25，30），[30，35]，频率分布直方图如图所示．已知生产的产品数量在[20，25）之间的工人有6位．
为了调查某厂2000名工人生产某种产品的能力，随机抽查了m位工人某天生产该产品的数量，产品数量的分组区间为[10，15），[15，20），[20，25），[25，30），[30，35]，频率分布直方图如图所示．已知生产的产品数量在[20，25）之间的工人有6位．
为了调查某厂2000名工人生产某种产品的能力，随机抽查了m位工人某天生产该产品的数量，产品数量的分组区间为[10，15），[15，20），[20，25），[25，30），[30，35]，频率分布直方图如图所示．已知生产的产品数量在[20，25）之间的工人有6位．