题目内容
 为了调查某厂2000名工人生产某种产品的能力,随机抽查了m位工人某天生产该产品的数量,产品数量的分组区间为[10,15),[15,20),[20,25),[25,30),[30,35],频率分布直方图如图所示.已知生产的产品数量在[20,25)之间的工人有6位.
为了调查某厂2000名工人生产某种产品的能力,随机抽查了m位工人某天生产该产品的数量,产品数量的分组区间为[10,15),[15,20),[20,25),[25,30),[30,35],频率分布直方图如图所示.已知生产的产品数量在[20,25)之间的工人有6位.(Ⅰ)求m;
(Ⅱ)工厂规定从生产低于20件产品的工人中随机的选取2位工人进行培训,则这2位工人不在同一组的概率是多少?
【答案】分析:(1)由频率的意义可知,每小组的频率= ,由此计算产品件数在[20,25)内的人数;
,由此计算产品件数在[20,25)内的人数;
(2)根据概率公式计算,事件“低于20件产品的工人选取2位”有15种可能,而且这些事件的可能性相同,其中事件“这2位工人不在同一组”可能种数是8,那么即可求得事件A的概率.
解答:解:(Ⅰ)根据直方图可知产品件数在[20,25)内的人数为m×5×0.06=6,
则m=20(位).(6分)
(Ⅱ)根据直方图可知产品件数在[10,15),[15,20),[20,25)组内的人数分别为2,4.
设这2位工人不在同一组为A事件,低于20件产品的工人选取2位有C62=15种,
这2位工人不在同一组的有2×4=8,
则 .
.
答:选取这2人不在同组的概率为 .(12分)
.(12分)
点评:此题考查了对频数分布直方图的掌握情况,考查的是概率的求法.如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)= .
.
 ,由此计算产品件数在[20,25)内的人数;
,由此计算产品件数在[20,25)内的人数;(2)根据概率公式计算,事件“低于20件产品的工人选取2位”有15种可能,而且这些事件的可能性相同,其中事件“这2位工人不在同一组”可能种数是8,那么即可求得事件A的概率.
解答:解:(Ⅰ)根据直方图可知产品件数在[20,25)内的人数为m×5×0.06=6,
则m=20(位).(6分)
(Ⅱ)根据直方图可知产品件数在[10,15),[15,20),[20,25)组内的人数分别为2,4.
设这2位工人不在同一组为A事件,低于20件产品的工人选取2位有C62=15种,
这2位工人不在同一组的有2×4=8,
则
 .
.答:选取这2人不在同组的概率为
 .(12分)
.(12分)点评:此题考查了对频数分布直方图的掌握情况,考查的是概率的求法.如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
 .
. 
练习册系列答案
 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
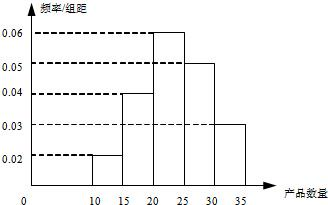 为了调查某厂2000名工人生产某种产品的能力,随机抽查了m位工人某天生产该产品的数量,产品数量的分组区间为[10,15),[15,20),[20,25),[25,30),[30,35],频率分布直方图如图所示.已知生产的产品数量在[20,25)之间的工人有6位.
为了调查某厂2000名工人生产某种产品的能力,随机抽查了m位工人某天生产该产品的数量,产品数量的分组区间为[10,15),[15,20),[20,25),[25,30),[30,35],频率分布直方图如图所示.已知生产的产品数量在[20,25)之间的工人有6位.
 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为 ,
, ,
, ,
, ,
, ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在
 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为 ,
,
 ,
, ,
, ,
, ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在