题目内容
20.已知命题$p:?{x_0}∈R,x_0^2+{x_0}-1<0$,则¬p为( )| A. | ?x∈R,x2+x-1≥0 | B. | $?{x_0}∈R,x_0^2+{x_0}-1>0$ | ||
| C. | $?{x_0}∉R,x_0^2+{x_0}-1≥0$ | D. | ?x∉R,x2+x-1>0 |
分析 利用特称命题的否定是全称命题写出结果即可.
解答 解:∵特称命题的否定是全称命题.
∴命题p:?x0∈R,使x02+x0-1<0的否定是:?x∈R,x2+x-1≥0.
故选:A
点评 本题考查命题的否定,注意量词的变化,基本知识的考查.

练习册系列答案
相关题目
12.已知$\overrightarrow a=({1,cosa}),\overrightarrow b=({sina,1})$,若$\overrightarrow a⊥\overrightarrow b$,则sin2α=( )
| A. | $-\frac{1}{2}$ | B. | -1 | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 1 |
5.圆心在x轴上,半径为2,且过点(1,2)的圆的方程为( )
| A. | (x-1)2+y2=4 | B. | (x-2)2+y2=4 | C. | x2+(y-1)2=4 | D. | (x-1)2+(y-4)2=4 |
12.已知$\overrightarrow{OA}=(1,1,0)$,$\overrightarrow{OB}=(4,1,0)$,$\overrightarrow{OC}=(4,5,-1)$,则向量$\overrightarrow{AB}$和$\overrightarrow{AC}$的夹角的余弦值为( )
| A. | $\frac{{\sqrt{26}}}{26}$ | B. | $\frac{{\sqrt{26}}}{12}$ | C. | $\frac{{3\sqrt{26}}}{26}$ | D. | $\frac{{2\sqrt{26}}}{13}$ |
9.已知θ是第一象限角,且$cosθ=\frac{{\sqrt{10}}}{10}$,则$\frac{cos2θ}{{sin2θ+co{s^2}θ}}$的值是( )
| A. | $\frac{8}{7}$ | B. | $-\frac{8}{7}$ | C. | $\frac{10}{7}$ | D. | $-\frac{10}{7}$ |
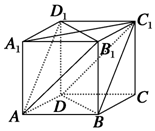 在正方体ABCD-A1B1C1D1中,如图.
在正方体ABCD-A1B1C1D1中,如图. 如图,矩形ABCD中,AB=2AD=2,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE,若M为线段A1C的中点,则在△ADE翻转过程中,对于下列说法:
如图,矩形ABCD中,AB=2AD=2,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE,若M为线段A1C的中点,则在△ADE翻转过程中,对于下列说法: