题目内容
若{an}是等比数列, ,则a1a2+a2a3+a3a4+…+an-1an=________.
,则a1a2+a2a3+a3a4+…+an-1an=________.

分析:用等比数列的性质可求得等比数列{an}的公比,再构造数列bn=an•an+1,利用等比数列的定义证明{bn}是等比数列,再求和即可.
解答:∵{an}是等比数列,
 ,设其公比为q,
,设其公比为q,则
 ,q=
,q= ,令bn=an•an+1,
,令bn=an•an+1,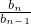 =
= (n≥2)又
(n≥2)又 ,
,∴{bn}是首项为8,公比为
 的等比数列,设其前n项和为Sn,则Sn-1=a1a2+a2a3+a3a4+…+an-1an=
的等比数列,设其前n项和为Sn,则Sn-1=a1a2+a2a3+a3a4+…+an-1an= ;
;故答案为:
 .
.点评:本题考查等比数列的性质,难点在于构造新数列bn=an•an+1,证明{bn}为等比数列,再求和,综合性强,属于中档题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
已知数列{an}的前n项和Sn=2n+k,若{an}是等比数列,则k的值为( )
A、-
| ||
| B、-1 | ||
| C、1 | ||
D、
|