题目内容
函数f(x)= (x∈[3,5])的值域为
(x∈[3,5])的值域为
- A.[2,3]
- B.[2,5]
- C.

- D.

A
分析:变形可得函数f(x)=(x-2)+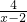 -2,令t=x-2可构造函数g(t)=t+
-2,令t=x-2可构造函数g(t)=t+ -2,t∈[1,3],通过求导数可得:函数g(t)的最小值为g(2)=2,最大值为g(1)=3,进而可得答案.
-2,t∈[1,3],通过求导数可得:函数g(t)的最小值为g(2)=2,最大值为g(1)=3,进而可得答案.
解答:变形可得函数f(x)= =
=
=(x-2)+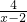 -2,令t=x-2,由x∈[3,5]可得t∈[1,3],
-2,令t=x-2,由x∈[3,5]可得t∈[1,3],
构造函数g(t)=t+ -2,t∈[1,3],令g′(t)=1-
-2,t∈[1,3],令g′(t)=1-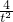 >0,
>0,
可得t>2,故可得函数g(t)在[1,2]上单调递减,在[2,3]上单调递增,
故函数g(t)的最小值为g(2)=2,最大值为g(1)或g(3)中的一个,
可得g(1)=3,g(3)= ,故最大值为g(1)=3,故g(t)∈[2,3]
,故最大值为g(1)=3,故g(t)∈[2,3]
故函数f(x)= (x∈[3,5])的值域为[2,3]
(x∈[3,5])的值域为[2,3]
故选A
点评:本题考查函数的单调性和导数的关系,涉及函数闭区间的最值的求解,属中档题.
分析:变形可得函数f(x)=(x-2)+
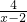 -2,令t=x-2可构造函数g(t)=t+
-2,令t=x-2可构造函数g(t)=t+ -2,t∈[1,3],通过求导数可得:函数g(t)的最小值为g(2)=2,最大值为g(1)=3,进而可得答案.
-2,t∈[1,3],通过求导数可得:函数g(t)的最小值为g(2)=2,最大值为g(1)=3,进而可得答案.解答:变形可得函数f(x)=
 =
=
=(x-2)+
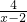 -2,令t=x-2,由x∈[3,5]可得t∈[1,3],
-2,令t=x-2,由x∈[3,5]可得t∈[1,3],构造函数g(t)=t+
 -2,t∈[1,3],令g′(t)=1-
-2,t∈[1,3],令g′(t)=1-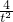 >0,
>0,可得t>2,故可得函数g(t)在[1,2]上单调递减,在[2,3]上单调递增,
故函数g(t)的最小值为g(2)=2,最大值为g(1)或g(3)中的一个,
可得g(1)=3,g(3)=
 ,故最大值为g(1)=3,故g(t)∈[2,3]
,故最大值为g(1)=3,故g(t)∈[2,3]故函数f(x)=
 (x∈[3,5])的值域为[2,3]
(x∈[3,5])的值域为[2,3]故选A
点评:本题考查函数的单调性和导数的关系,涉及函数闭区间的最值的求解,属中档题.

练习册系列答案
相关题目